SIFT特征提取算法理解与实现

我又回来了, 总算熬到放假了. . . 按照国际惯例先凑字数扯点近况.

没想到我托更的原因竟然不是懒, 而是事多. 最近几个礼拜真是累的够呛, 没想到研一课还挺多, 还都得做报告, 台下强制提问, 这感觉就有点过分了. 所以大家基本一份报告”吃遍天下”. 我还有几个报告在年后(1年3学期制), 所以有预感这个寒假也. . .

但总算是获得了一个喘息的机会, 然后平时娱乐也就打打麻将什么的, 也算正式入日麻坑了. 日麻这个事最开始的认识也是拜Vespa菊苣所赐, 后来看《赌博堕天录》中社长和开司玩的麻将游戏—地雷游戏, 为了看懂了解了下日麻规则. 毕业闲下来的时候随便打打日麻, 只在天极牌和雀姬上玩过一段时间. 到了这学期, 需要频繁地在延长与宝山来回跑, 在路上就靠打牌打发时间了. 话说最近雀魂又莫名开始火起来了, 台游雀姬联合B站看准时机看来也要插一脚. 不过雀魂做得确实不错, 页游的形式很灵活方便.

另一个由于之前关注的几个漫画出了动画, 特别是《约定的梦幻岛》(在上一期漫画推荐中也有提到), 所以冲了个大会员来看, 顺便bilibili漫画与网易版权合作, 也能继续看漫画版了. 看来作者也要开始收笔完结了, 最近一话诺曼出场了/(ㄒoㄒ)/~~

另外之前七牛云终究还是崩了, 网站图片全挂(不蒜子也被阴了一把), 于是干脆把图片也挂到Github上了, 虽然速度堪忧, 先勉强用用. 然后本站音乐外链也全换成了网易云, 虾米的外链太慢, 官方似乎也有意阉割外链功能.

---

说回正题, 这个学期一直忙着上课(听报告╮(╯-╰)╭)和项目, 其实留给自己折腾的时间很少. 其中有一门CVPR的课, 一个课程项目是图像特征提取, 所以就去了解了下SIFT. 其作者Lowe的论文对于算法具体实现叙述很少, 虽然CSDN上相关文章一大堆, 但真正搞懂且说明白的人也不多. 我在理解与实现中帮助比较大的是这两位博主cig01和zhaocj, 博主zhaocj写了一篇33页的文章, 详尽讲解了SIFT原理与openCV的SIFT实现, 我在最后才看到这篇文章, 此前自己已经理解过openCV的源码, 但那篇文章还是在一些细节上给了我启发, 鉴于资源网上不太好找, 就分享个网盘(m981)吧, 另外这是我做的ppt.

按理说已经有很多人写过SIFT, 就没我等渣渣什么事了, 但我确实在这上花了比较多的时间, 理解原理, 然后用Matlab与C++实现了SIFT, 过程中碰到的问题及处理细节还是印象深刻的. 所以这篇博文我主要还是会重点讨论其他博主所忽视的实现上的细节问题, 算作一个补充. 目测可能会比较长. . .

---

SIFT的理解

关于SIFT

SIFT即Scale Invariant Feature Transform, 由英国哥伦比亚大学计算机系教授Lowe在1999年首次提出, 并在04年完善后发表了成果《Distinctive Image Features from Scale-Invariant Keypoints》.

SIFT简单来说就是一种稳定、高效的图像关键点检测与描述子生成方法, 如同其名字中所描述的, SIFT特征具有对旋转、尺度缩放、光照变化的不变性, 同时对3D视角变化、仿射变换、加性噪声也保持一定程度的稳定性. 在SIFT之前的一些方法(各种角点检测(Corner detection)方法, 如Moravec角点检测, Harris角点检测等)是不具有尺度不变旋转不变的. 在SIFT之后的06年, Bay等在SIFT基础上改进, 提升其检测效率, 提出了SURF(Speeded Up Robust Features, 加速鲁棒性特征)算法. 09年G.Yu和 J.M. Morel在SIFT基础上提出Affine-SIFT (ASIFT)以此改善SIFT特征的仿射不变性能. 应该来说, SIFT作为一种经典的关键点检测算法, 在计算机视觉领域动不动就是深度学习模型的当下仍然有着存在感, 或许SIFT本身所包含的尺度不变的思想仍有借鉴意义. 之前看到有基于深度学习的关键点检测方法LIFT出来, 从实验结果来看SIFT的性能依然不错.

另外Lowe为SIFT申请了专利, 在07年的时候提出了基于SIFT的图像拼接方法AutoStitch(Automatic Panoramic Image Stitching using Invariant Features), 这又是图像拼接领域的里程碑式的方法.

具体到SIFT主要的两部分即关键点检测与关键点描述.

关键点检测

这一部分的目的就是检测关键点. 在SIFT中关键点来源于DoG图像的极值点, 然后经过筛选过程去除不稳定的极值点后剩下的就作为关键点了.

建立图像金字塔

图像金字塔是图像多分辨率分析或者说不同尺度空间分析的工具, 在SIFT中使用了图像金子塔, 这是其尺度不变性的一个重要来源. SIFT与其他关键点检测算法的不同之处就在于引入了尺度空间(Scale space), 在图像的行列坐标外, 还多了一个尺度空间的坐标$\sigma​$, 这个坐标来源于对图像做了方差为$\sigma​$的高斯滤波或$\sigma​$的图像尺度缩放.

为实现多尺度, 在SIFT中需要构建两个金字塔, 高斯模糊金字塔与DoG金字塔. 这里是先构成高斯模糊金字塔, 在以此构建DoG金子塔的关系, 我们需要的极值就是在DoG金子塔中寻找.

那怎么构建高斯模糊金子塔呢? 为与论文叙述统一, 将金子塔的每一层称为octave, 而一层中的一张张图像称作layer, 构建金字塔的具体做法是对初始图像做不同尺度$\sigma$的高斯模糊生成第一个octave(底层), 下一个octave的第一张图像由上一个octave最后一张图像降采样产生(长宽减半, 具体方法的话在openCV源码中使用了最近邻), 接着对这第一张图像同样做不同尺度高斯模糊产生当前octave其余图像, 而下一octave重复进行以上操作. 至于DoG金子塔建立则更简单了, 其每个octave的图像即对高斯模糊金字塔对应octave内图像相邻图像两两做差得到(注意图像做差操作会使像素值变负, 在实现时转换为合适类型). 这样我们知道如果DoG金子塔一octave内有$s$张图像, 则高斯模糊金字塔octave有$s+1$张.

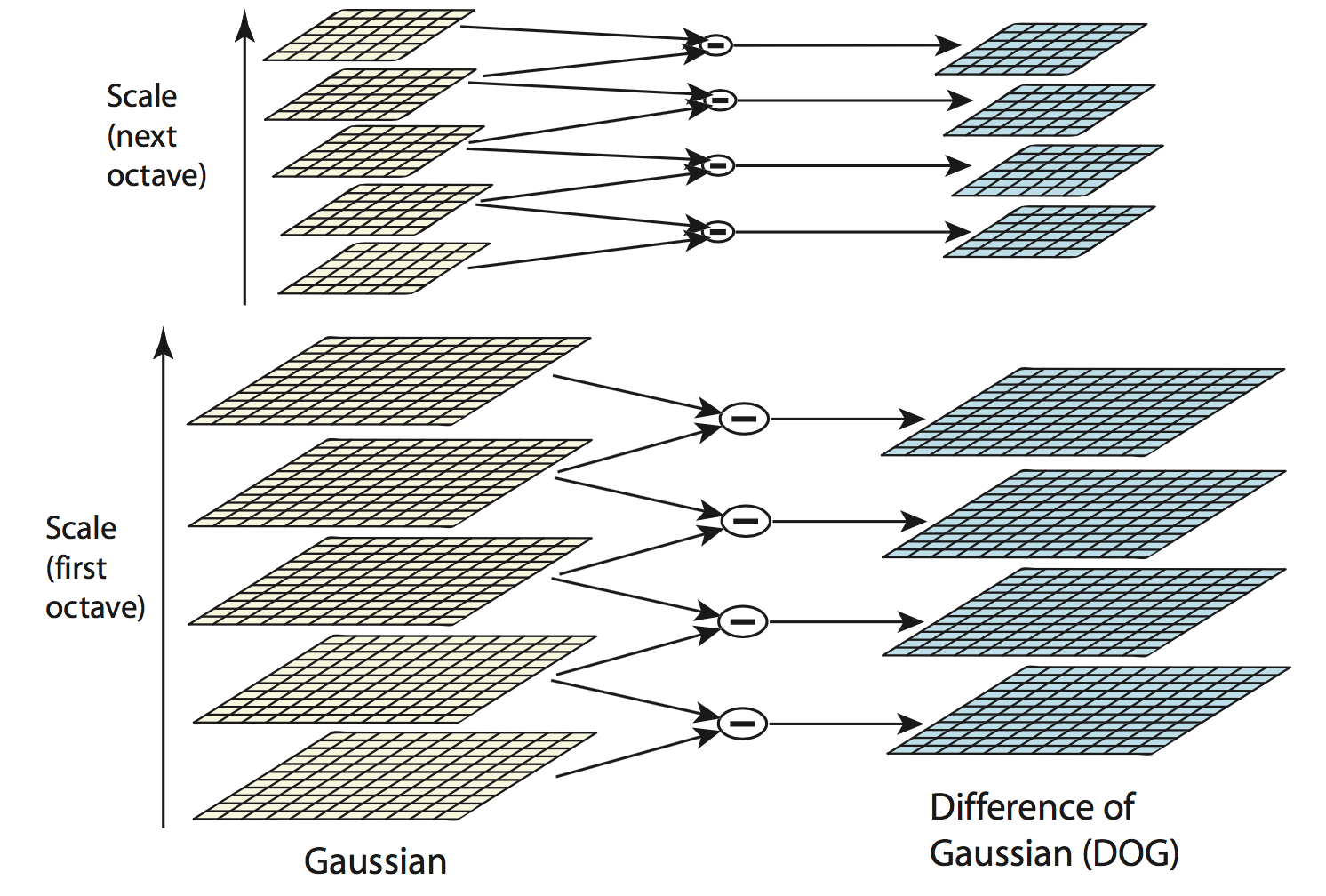
接下来我们就面临几个具体问题, 比如金子塔octave取多少? 金子塔octave内图像数$s$又取多少? 高斯模糊金字塔第一个octave的第一个图像的尺度空间坐标$\sigma_0$取多少呢?

对于octave可以取比较好的实验值, 事实上实验结果来看, 极值点主要出现在前几个octave中, 过大的octave没有意义. 在具体的实现中, 我有看到是用下面公式计算得到的

$$Octave = log_2(min(w_0, h_0)) - log_2(min(w, h))+1$$

$w_0​$与$h_0​$为原图像宽高, $w​$与$h​$为塔顶图像宽高. 如对于一幅大小为16×16的图像, 当塔顶图像设定为4×4时, 金字塔层数octave = 3. 可以对其验证, 如前所述, 每一个octave的图像尺寸是前一个octave图像尺寸的一半, 于是16->8->4, 可见确实是三层的图像金字塔.

至于$s$的取值同样是实验值, Lowe的实验结果说明取3为优. 如前所述, $s$为DoG金子塔octave内的图像数目, 我们假设一octave图像在尺度空间上由$\sigma$均匀变化到$2\sigma$, 这样相邻两张图像尺度比值为一定值$k$

$$k=2^{\frac{1}{s}}$$

如此一来, 实现了DoG图像在尺度空间坐标的连续性, 即当前octave最后一张DoG图像与下一个octave的第一张DoG图像的尺度比值也是$k$.

至于$\sigma_0$同样也是实验值, 在Lowe的实验中取1.6为优. 当$\sigma_0$与$k$都确定后, 金字塔中的每一张图像在尺度空间的坐标就都确定了.

另外为了获取更多的极值点, 通常会先对原图像做插值(论文中为双线性插值), 将图像的尺寸扩大一倍再作为初始图像进行后续处理.

番外 关于LoG与DoG

这一部分简单聊聊DoG. 在SIFT中关键点检出使用的是DoG(Difference of Gaussian), DoG被证明是LoG(Laplacian of Gaussian)的良好近似. 这部分在《数字图像处理 第三版》P.459关于图像边缘检测算子中有涉及到.

LoG是Marr和Hildreth在1980年提出的边缘检测算子, 其本质上是二阶导数的近似(边缘检测算子可用二阶导数), 另一方面LoG算子可以自由调整大小, 在任何图像尺度上都能取得比较好的检测效果. LoG形式上可对二维高斯函数的二阶导数进行采样得到.

$$L(x,y,\sigma) = G(x,y,\sigma)\ast I(x,y)$$ $$G(x,y, \sigma) = \frac{1}{2\pi\sigma^2}\exp\left(-\frac{(x^2+y^2)}{2\sigma^2}\right)$$

但LoG的缺点是为了求得零交叉点(Laplace算子通过对图像求取二阶导数的零交叉点(zero-cross)来进行边缘检测)需要经过比较麻烦的像素比较操作. 于是Marr和Hildreth在当时提出用DoG(高斯差分)近似LoG的运算. DoG函数定义如下

$$D(x,y,\sigma) = L(x,y,k\sigma) - L(x,y,\sigma)$$

故在构建DoG金子塔时是对不同尺度高斯模糊后的图像做差来产生DoG图像.

番外 高斯函数卷积性质

在构建高斯模糊金子塔时有一个细节, 比如一octave假设各图像尺度空间坐标为$\sigma_0, k\sigma_0$, 这意味着此octave中的图像是对初始图像分别做方差为$\sigma_0,k\sigma_0$的高斯模糊得到的, 在这种情况下, 我们是视初始图像的空间尺度坐标为0, 但尺度空间的建立不能从尺度为0开始(尺度坐标是成比例增长, 起始不能为0, 另一种解释是在尺度空间理论中视尺度坐标为0时图像是无限精细不可获得), 故在Lowe的论文中假设我们获得的初始图像是已经经过了方差为0.5的高斯模糊处理.

那么此时我们的问题变成如何从尺度为$\sigma_0$的图像得到尺度为$\sigma_1$与尺度为$\sigma_2$的图像, 用式子来描述就是

$$I(x,y,\sigma_0)=I(x,y)*G(x,y,\sigma_0) \\ I(x,y,k\sigma_0)=I(x,y)*G(x,y,k\sigma_0)$$

利用高斯函数的卷积性质

$$G(x,y,k\sigma_0)=G(x,y,\sigma_0)*G(x,y,\sqrt{(k\sigma)^2-\sigma^2})$$

我们有

$$I(x,y,k\sigma_0)=I(x,y,\sigma_0)*G(x,y,\sqrt{(k\sigma_0)^2-\sigma_0^2})$$

顺便一说, 这个性质可以使用傅里叶的卷积性质来证, 具体可参考《Products and Convolutions of Gaussian Probability Density Functions》, 证明过程也比较简洁这里就不重复写了.

寻找局部极值点

构造完DoG金字塔后, 就可以寻找极值点了. 具体来说, 把同一octave经过不同尺度高斯滤波后的图像按尺度大小堆成一叠(如下图), 若当前像素值(×)比邻近的26个位置(包括相邻上下两张图像)都大, 则作为一个局部极大值, 同样可以找到局部最小值.

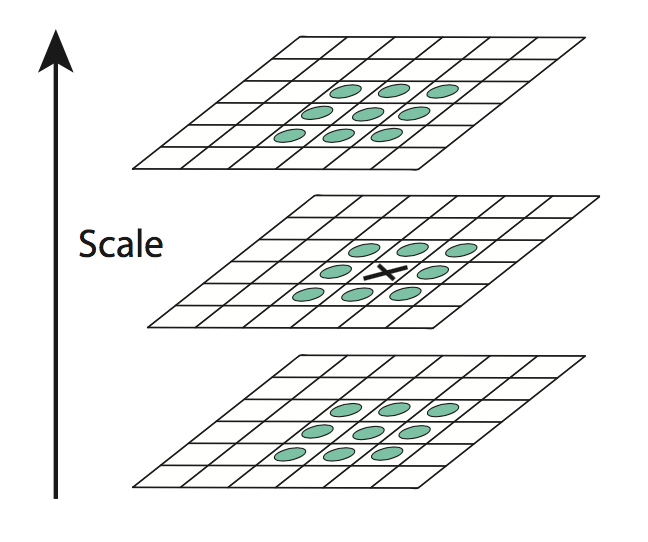
这里比较求局部极值点引出了另一个细节问题, 即一个octave中的第一张图像与最后一张图像中的像素无法进行3×3的比较得到极值, 如果是按之前说的高斯模糊金字塔每octave生成$(s+1)$张图像, 做差值后将生成$s$张DoG图像, 那么极值的寻找实际只在$(s-2)$个尺度上进行.

为了在每层中检测$s$个尺度的极值点, 简单粗暴的做法是再补上两张高斯模糊后的图像, 也就是高斯模糊金字塔一个octave生成$(s+3)$张图像, 然后在$s+1$张DoG图像的第2张到倒数第2张之间的图像像素中去寻找极值点. 如下图

同时为了保证之前DoG图像尺度坐标变化的连续性, 在降采样建立高斯模糊金字塔时, 每一个octave的第一张图像由前一个octave的倒数第三张图像降采样得到(原来是使用最后一张).

番外 寻找极值点的实现细节

在openCV的源码中, 判断极值点的第一步是看其是否高于一个阈值, 像素点过小的点会直接忽略. 在进行像素值比较时使用的是大于等于与小于等于, 这样能够检测到更多的极值点.

局部极值点筛选

这一步的主要目的是对之前得到的极值点进行测试, 看其是否足够稳定. 主要进行如下两步, 极值点精确定位与消除边缘效应.

极值点精确定位

由于之前所找的极值是在离散空间中进行的, 所以找到的极值未必与真实极值位置相同. 论文提出可以通过对尺度空间DoG函数进行曲线拟合寻找极值点来减小这种误差. 利用已知的离散空间点插值得到的连续空间极值点的方法叫做子像素插值(Sub-pixel Interpolation).

这里有一个一元函数的例子说明求精确极值原理, 参考博文.

方法中用到了泰勒(Taylor)展开, 一元函数形式在$x_{0}$的泰勒展开公式如下

$$f(x) \approx f(x_0)+(x-x_0)f'(x_0)+\frac{1}{2!}(x-x_0)^2f''(x_0)$$

而对于二元函数, $f(x, y)$在$(x_{0}, y_{0})$处泰勒展开式为

$$f(x,y)\approx f(x_0,y_0)+[(x-x_0)f'_x(x_0,y_0)+(y-y_0)f'_y(x_0,y_0)] \\ +\frac1{2!}\left[(x-x_0)^2f''_{xx}(x_0,y_0)+(x-x_0)(y-y_0)f''_{xy}(x_0,y_0) \\ +(x-x_0)(y-y_0)f''_{yx}(x_0,y_0)+(y-y_0)^2f''_{yy}(x_0,y_0)\right]\\$$

上式可写成向量形式, 注意$dx=x-x_0$, $dy=y-y_0$

$$f(x, y)\approx f(x_0, y_0)+[dx\ \ dy]\left[ f_x(x_0,y_0) \atop f_y(x_0,y_0)\right] \\ +\frac{1}{2!}[dx\ \ dy]\left[ f_{xx}(x_0,y_0)\ \ f_{xy}(x_0,y_0) \atop f_{yx}(x_0,y_0)\ \ f_{yy}(x_0,y_0)\right]\left[ dx \atop dy\right]$$

若令$\boldsymbol{x}=\left[x \atop y\right]$, 且$\boldsymbol{x}_0=\left[x_0 \atop y_0\right]=\boldsymbol{0}$, 有

$$f(\boldsymbol{x})\approx f(\boldsymbol{x}_0)+\left.\frac{\partial f^{T}}{\partial\boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}\boldsymbol{x}+\frac{1}{2!}\boldsymbol{x}^{T}\left.\frac{\partial^{2} f}{\partial\boldsymbol{x}^2}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}\boldsymbol{x}$$

同样这里是对$D(x,y,\sigma)$进行泰勒展开, 如果写成向量形式则$\boldsymbol{x}$是三维列向量, 同样这里$\boldsymbol{x}_0=\boldsymbol{0}$

$$D(\boldsymbol{x})\approx D(\boldsymbol{x}_0)+\left.\frac{\partial D^{T}}{\partial\boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}\boldsymbol{x}+\frac{1}{2!}\boldsymbol{x}^{T}\left.\frac{\partial^{2} D}{\partial\boldsymbol{x}^2}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}\boldsymbol{x}$$ $$\frac {\partial D}{\partial \boldsymbol{x}} = \begin{bmatrix} \frac {\partial D}{\partial x} \\ \frac {\partial D}{\partial y} \\ \frac {\partial D}{\partial \sigma}\end{bmatrix} = \begin{bmatrix} \frac {D(x+1,y,\sigma) - D(x-1,y,\sigma)}{2} \\ \frac {D(x,y+1,\sigma)-D(x,y-1,\sigma)}{2} \\ \frac {D(x,y,\sigma+1) - D(x,y,\sigma-1)}{2} \end{bmatrix}$$ $$\frac{\partial^2 D}{\partial \boldsymbol{x}^2} = \begin{bmatrix} D_{xx} & D_{xy} & D_{x\sigma} \\ D_{yx} & D_{yy} & D_{y\sigma} \\ D_{\sigma x} & D_{\sigma y} & D_{\sigma\sigma} \end{bmatrix}$$

其中

$$D_{xx}=\frac { \frac{D(x+1,y,s)-D(x,y,s)}{1} - \frac{D(x,y,s)-D(x-1,y,s)}{1} }{1}$$ $$D_{xy} = \frac { \frac{D(x+1,y+1,s)-D(x-1,y+1,s)}{2} - \frac{D(x+1,y-1,s)-D(x-1,y-1,s)}{2} }{2}$$

为求极值, 两边对$\boldsymbol{x}$求导, 并令其为0, 这部分需要用到数量函数对向量变量求导的知识(可参考博文矩阵求导与Matrix calculus)

$$\begin{align} \frac{\partial D}{\partial\boldsymbol{x}}&=\left.\frac{\partial D^T}{\partial\boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}+\frac{1}{2}\left(\left.\frac{\partial^2 D}{\partial\boldsymbol{x}^2}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}+\left.\frac{\partial^2 D^T}{\partial\boldsymbol{x}^2}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}\right)\boldsymbol{x} \\ &=\left.\frac{\partial D^T}{\partial\boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}+\left.\frac{\partial^2 D}{\partial\boldsymbol{x}^2}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}\boldsymbol{x}\\ &=\boldsymbol{0} \end{align}$$

可解出精确极值点$\boldsymbol{x}$

$$\hat{\boldsymbol{x}}=-\left.\frac{\partial^2 D^{-1}}{\partial\boldsymbol{x}^2}\frac{\partial D}{\partial\boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}$$

于是可求出精确极值$D(\hat{\boldsymbol{x}})$.

$$D(\hat{\boldsymbol{x}})\approx D(\boldsymbol{x}_0)+\frac{1}{2}\left.\frac{\partial D^{T}}{\partial\boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{x}_0}\hat{\boldsymbol{x}}$$

这里再说明一下, 事实上这里的$\boldsymbol{x}$准确说应该是极值点$\boldsymbol{x}$与$\boldsymbol{x}_0$的差值, 即极值点的偏移量$\boldsymbol{x}-\boldsymbol{x}_0$, 但由于这里假设了$\boldsymbol{x}_0=\boldsymbol{0}​$所以才得到上述结果.

接下来就是根据计算出的精确极值筛选之前找到的极值点了, 主要基于两点: 一是之前找到的极值点偏离精确极值点的程度, 二是找到精确极值点极值的幅度大小.

对于第一点, 只要精确极值点在任意方向$(x, y,\sigma)$偏离找到的极值点某个阈值则剔除该极值点, 通常这个阈值在论文中取0.5; 对于第二点, 只要$|D(\hat{\boldsymbol{x}})|$小于某个阈值则剔除该极值点, 响应值过小易受噪声干扰, 视为不稳定点, 通常这个阈值在论文中取0.03(图像灰度归一化为[0,1]). 下面是经过这一步筛选前后的效果

消除边缘效应

利用DoG得到的极值点还有另一个问题, 之前说LoG是对二阶导数的近似, 而DoG又是LoG的近似, DoG的处理会使得边缘像素点的响应很大(边缘效应), 接下来就是要尽可能地去除边缘关键点, 而保留下其他信息较大的点如角点.

为了找到和去除那些边缘响应过大的像素点, 需要利用那些像素点在DoG响应曲面(准确说是空间离散点集)上的特性. 比如曲面在该像素点处两主曲率(Principal curvature)的差值会很大(大的主曲率会很大, 小的主曲率会很小), 而对于角点的关键点两主曲率差值较小(大的主曲率与小的主曲率都会很大).

由于两主曲率与极值点处的Hessian矩阵特征值成比例(微分几何结论, 关于主曲率相关知识可参考这个), 同时我们将考察两主曲率的差值转化为考察比值, 这样可以利用矩阵特征值性质去求而避免了直接去求Hessian矩阵特征值.

Hessian矩阵定义:

$$H(D(\boldsymbol{x}))\overset{def}{=}\frac{\partial^{2} D(\boldsymbol{x})}{\partial\boldsymbol{x}\partial\boldsymbol{x}^T}=\begin{bmatrix} D_{xx} & D_{xy} \\ D_{xy} & D_{yy} \end{bmatrix}$$

设Hessian矩阵的两特征值为$\alpha, \beta$, 且$\alpha>\beta$, 令$\alpha=\gamma\beta$有

$$\begin{aligned} \text{tr} (H) &= D_{xx} + D_{yy} = \alpha + \beta \\ \det (H) &= D_{xx}D_{yy} - (D_{xy})^2 = \alpha \beta \end{aligned}$$ $$\frac{\text{tr}(H)^2}{\det(H)} = \frac{(\alpha + \beta)^2}{\alpha \beta} = \frac{(\gamma \beta + \beta)^2 }{\gamma \beta^2} = \frac{(\gamma+1)^2}{\gamma} = \gamma+\frac{1}{\gamma}+2$$

上式当两特征值相同时即$\gamma=1$时最小, 当两特征值差越大, 上式值也越大. 所以可以用$\gamma$再设置一个阈值, 间接地排除两主曲率相差悬殊的关键点(即边缘响应较大的关键点), $\gamma$这个阈值在Lowe论文中设置为了10.

番外 在极值点筛选过程实现上的细节

这一步总得来说细节比较少, 首先需要注意的是一阶, 二阶, 二阶混合离散导数的计算, 特别注意这些导数的分母, 另外在进行阈值判断时需要注意是否需要将像素值归一到[0,1].

在openCV的实现源码中, 求精确极值时并不是偏移量超过阈值就之间去除, 而是会有5次调整机会, 即原坐标加上偏移后再按如上步骤计算偏移看是否这次满足阈值. 实现在一些阈值上也有些许改动.

关键点描述

经过筛选考验的极值点就作为关键点保留下来了, 接着我们需要对每个关键点生成一个描述信息或称为描述子(Descriptor). SIFT作为一种局部特征, 即在计算描述子时需要用到关键点周围邻域的像素信息. 但在此之前需要给每个关键点分配一个主方向.

关键点主方向

给关键点分配主方向也是SIFT区别于其他特征的地方, 是SIFT特征拥有旋转不变性的原因之一. 关键点的主方向确定了在计算特征描述时使用的是关键点邻域内的哪些像素. 具体做法如下,

对于某一个关键点所在尺度$\sigma​$的高斯滤波后的图像可表达为

$$L(x,y, \sigma) = G(x,y, \sigma) \ast I(x,y)$$

计算以关键点为中心, 以$3 \times \sqrt{2} \sigma​$(为了圆域包含内接正方形)为半径的区域(圆域)内的所有图像像素点的梯度幅角和幅值, 图像某点处梯度定义为

$$grad\ L(x,y, \sigma)=\begin{bmatrix} \frac{\partial L}{\partial x} \\ \frac{\partial L}{\partial y} \end{bmatrix}$$

梯度幅角与幅值计算公式如下

$$\begin{aligned} m(x,y) & = \sqrt{(L(x+1,y) - L(x-1,y))^2 + (L(x, y+1) - L(x, y-1))^2} \\ \theta(x,y) &= \arctan \left(\frac{L(x, y+1) - L(x, y-1)}{L(x+1,y) - L(x-1,y)} \right) \end{aligned}$$

完成关键点邻域内梯度幅角与幅值计算后, 将幅角的360°每10°为一个区间划分作为横轴, 共36个区间, 纵轴为在对应幅角区间内的像素点幅值累加, 可做出方向统计直方图.

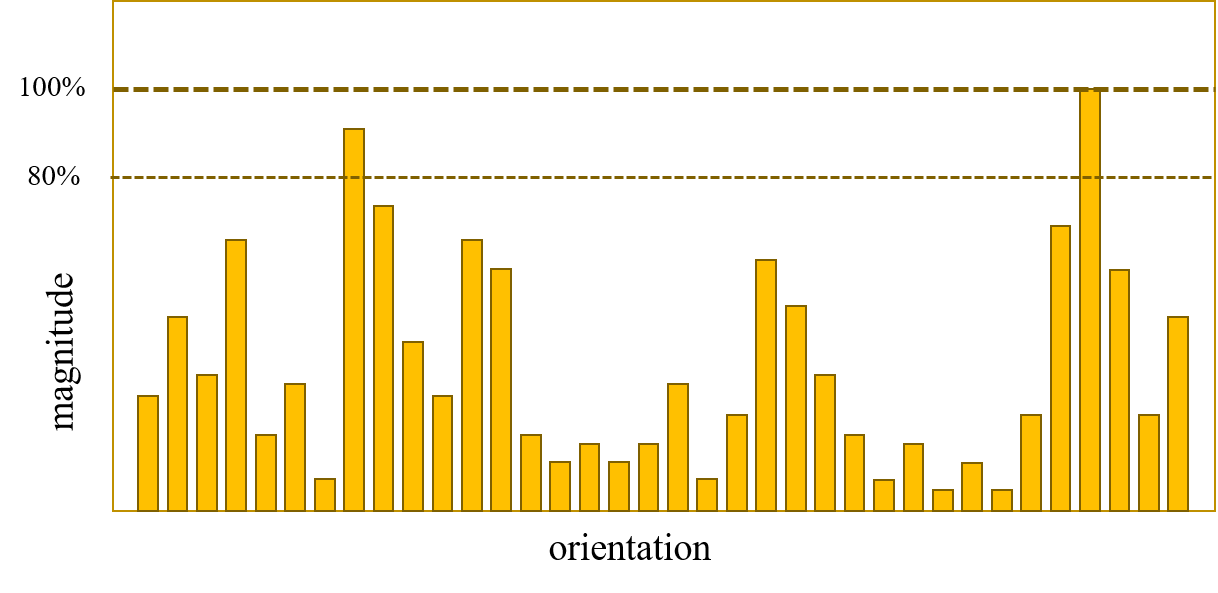
为改善特征仿射不变性的性能, 一般将累加的像素点幅值用高斯函数加权, 高斯加权函数的$\sigma​$取为关键点尺度的1.5倍. 经过高斯加权即让靠近关键点的像素幅值具有更大的权重(以此改善仿射不变性).

先对得到的直方图进行平滑(如加权滑动平均), 然后将直方图的峰值对应的幅角即作为该关键点的主方向(dominant orientation). 此时得到的主方向为一个10°区间的范围, 需要进行插值拟合(如抛物线拟合), 从离散值直方图得到较精确的关键点主方向.

如果像上图这样, 有另一个峰值超过最高峰值的80%, 那么这个方向应该作为一个参考的辅方向保留. 在实际操作中, 就直接把关键点再复制一份(拥有与原关键点相同的尺度与位置), 新关键点的主方向取这个参考的辅方向. 一个关键点是可能有多个辅方向的.

特征向量生成

一个关键点点所包含的信息由特征描述子(Feature Descriptor)数值描述. 在SIFT中, 特征描述子是从关键点与其主方向确定的区域提取得到的一个128维特征向量.

为了确定最后提取特征向量需要的像素, 首先要确定提取特征向量的像素区域大小. 将以关键点为中心的邻域划分成 $4\times 4$个子区域, 每个子区域的尺寸为3σ(3$\sigma$原则)个像素, $\sigma$即关键点所在图像尺度空间坐标.

确定特征提取像素区域

确定了提取特征的像素区域(方域)大小后, 还要确定提取特征区域以关键点为中心的旋转角度. 为便于说明, 在提取特征向量的区域建立坐标轴, x轴正向朝右, y轴正向朝下, 而坐标原点位于关键点处. 在此坐标轴下, 比如计算特征向量像素区域(这是一个方域)的最左上角位置的坐标为$(x, y)$(注意这是以关键点为原点的相对坐标). 接着将计算特征向量像素区域顺时针旋转至该关键点的主方向(如图), 旋转后之前最左上角的像素坐标变为$(x’, y’)$. 这个过程可由坐标变换公式描述为

$$\left[ \begin{matrix} x’\\ y’\end{matrix} \right] = \left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{matrix} \right] \left[ \begin{matrix} x\\ y \end{matrix} \right]$$

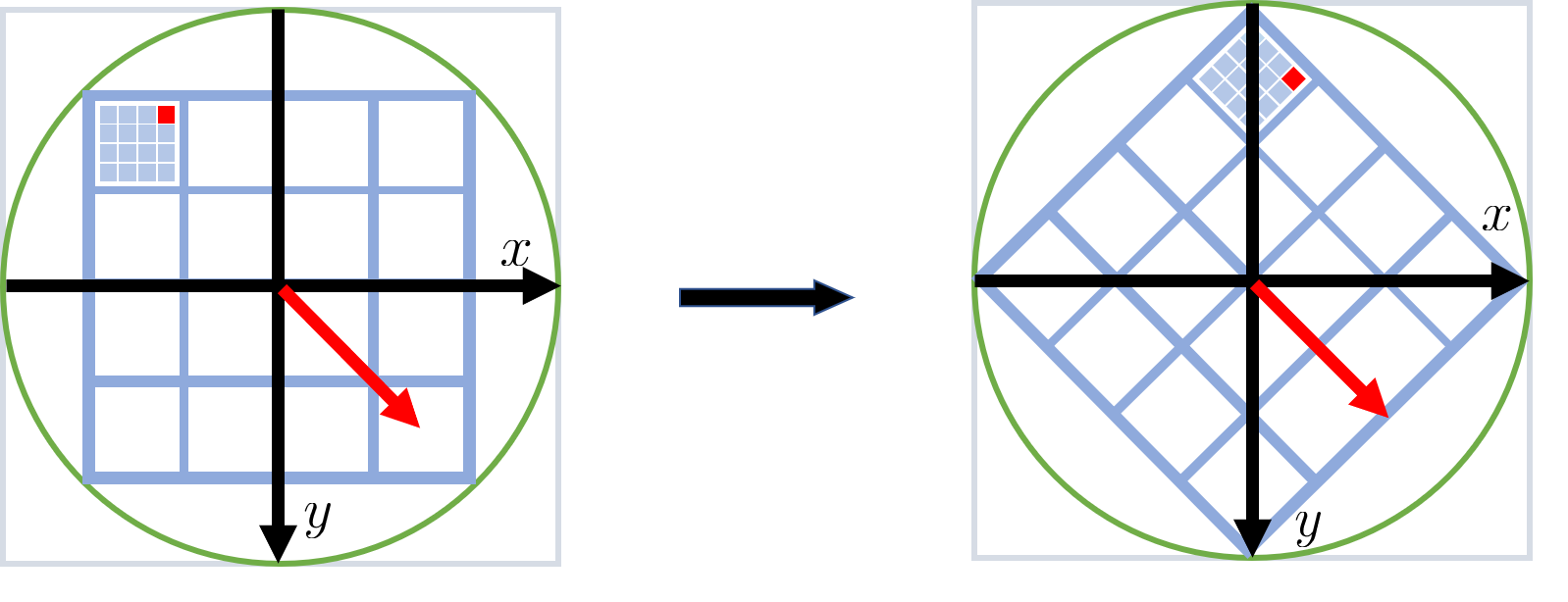
用上式就可以通过遍历旋转前区域内像素坐标值, 经上式转化后, 即遍历的是区域旋转后的像素位置, 这样避免了直接去求旋转后区域内的像素坐标.

计算特征向量

特征向量的计算依旧需要用到统计梯度直方图. 具体来说, 统计$4\times4$个子区间内像素(16个像素)的梯度(幅值与幅角), 与之前相同, 将幅角从360°每45°为一个区间划分作为横轴, 共8个区间, 纵轴为在对应幅角区间内的像素点幅值累加, 以此作出统计直方图.

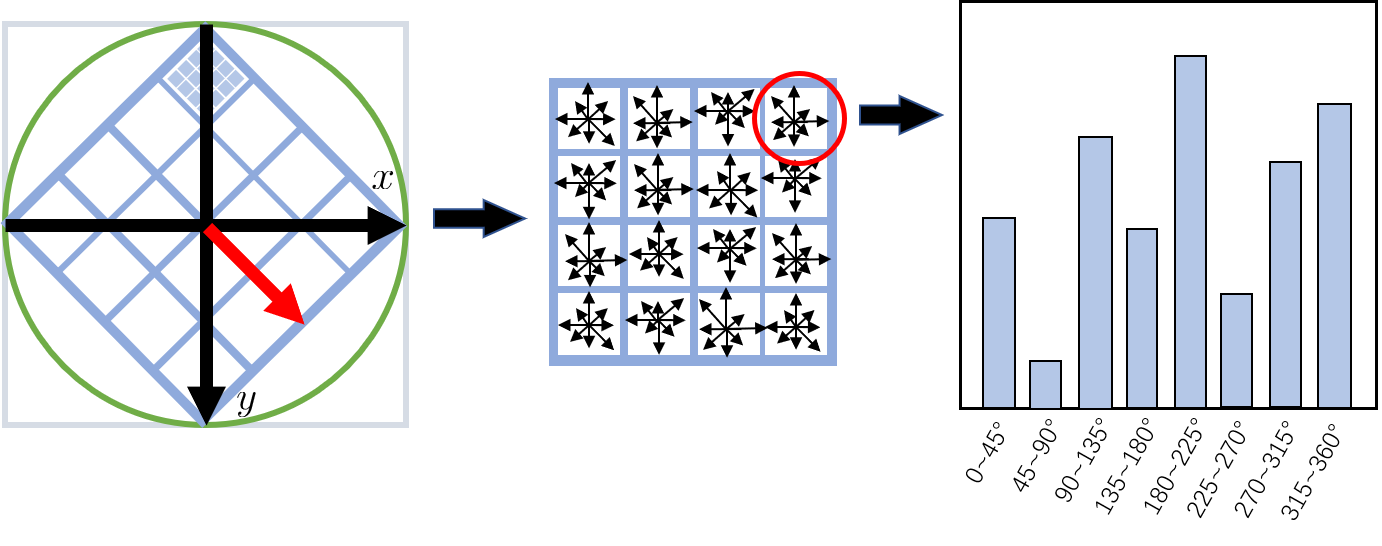
这样每个子区域都包含8个柱状图的信息, 所以对于一个关键点可提取$4\times 4\times8$共128维的特征向量.

这里有比较多的细节问题, 首先注意计算主方向时的邻域范围与计算特征向量时是不同的, 至于具体怎么取取决于实现.

另外一个比较难理解的地方是直方图的插值问题. 此处我们有三个坐标, 即除图像行列外还有一个梯度幅角的坐标, 故使用三线性插值来处理. 这意味当一个像素点落在某个子区域时, 我们其实并不是直接将该像素点的梯度幅值加到所属子区域的方向直方图中, 而是通过某种方式得到权值, 通过权值贡献到离该像素点幅值最近的4个子区域的直方图, 这里计算权值的方式就是利用了三线性插值的性质. 不仅是贡献到4个子区域有权值, 而且离像素梯度幅角最近的两个角度区间也需要计算权值. 直观上来说的话, 类似于我们得到了立方体内一点的值, 将其值贡献到其8个顶点上去.

番外 关于三线性插值

一般意义上的三线性插值(Trilinear interpolation)指的是已知空间8个点的值, 去得到以8个点为顶点的长方体内任意一点的值, 本质上是连续进行7次线性插值得到内点的值.

在这里, 更像是三线性插值的逆用(或者有更专业的说法?), 已知空间一点的值得到包含该点立方体8个顶点的值. 利用三线性插值的性质, 可以求出分配到各顶点的权值.

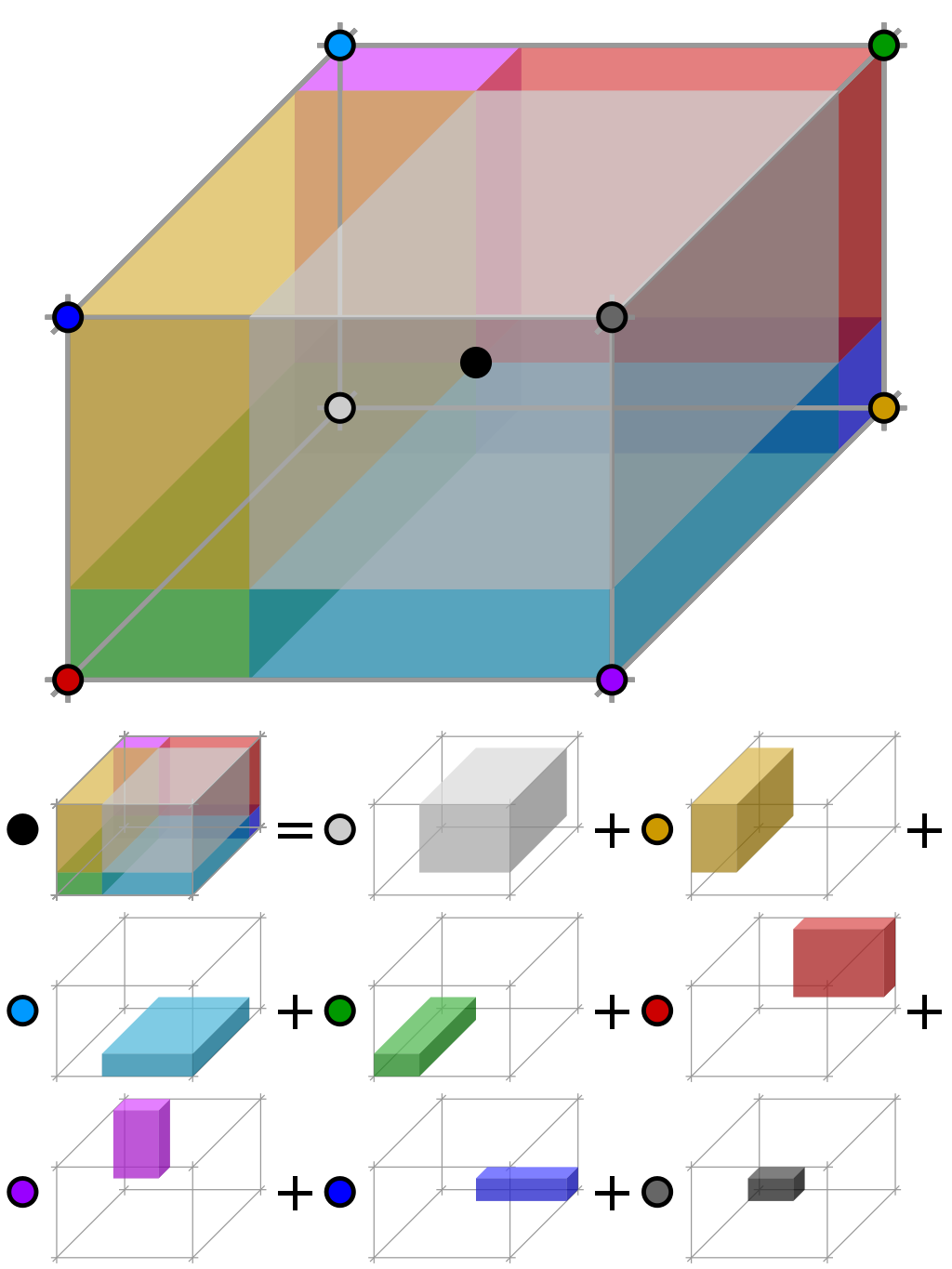
如上图所示, 像素点作为内点, 其对邻近四子区域幅度权值为以内点到顶点连线为体对角线的长方体体积占8顶点构成长方体体积之比.

特征向量的优化

为了改善特征受光照条件的影响, 需要对特征向量做优化. 对于线性光照改变, 由于SIFT使用的是DoG, 故特征对于对比度变化天生具有鲁棒性, 对于改善光照强度影响这里的处理是对特征向量进行归一化处理. 而对于非线性的光照改变, 只能通过抑制过大的特征向量的分量来改善, 使特征向量各分量差距不过于悬殊.

SIFT的实现

我一开始是用Matlab初步实现了SIFT算法, 完成调试后又用C++进行重写, 尽可能地保留程序的易读性, 在部分具体实现中参考了openCV中对SIFT的优化改进方法, 包括阈值的设定, 一些特定变量的使用(如利用Mat进行矩阵运算). 但总得来说, 效率上依然不如openCV, 或许还有改进空间. 代码放在GitHub, 在openCV3.4环境下正常运行.

参考

• Lowe1999年论文《Object Recognition from Local Scale-Invariant Features》

• Lowe2004年完善SIFT后的论文《Distinctive Image Features from Scale-Invariant Keypoints》

• SIFT wiki

• 图像特征比对(一)-取得影像的关键点 关键点检测一些概念的理解

• Local Invariant Feature Detectors
  .
  .
  .
  .
  .
  .
  .
  .
  .
  .
  .
  終わり