关于采样的总结

最近又在复习信号处理的东西, 对于一些内容有了更深入的理解, 于是做一个关于采样的总结. 众所周知, 自然界大多数信号是模拟信号, 采样是数字系统处理的第一步, 主要由各种传感器配合A/D来实现. 在FFT为什么那么快一文中提到了“重采样”的概念, 在那里一笔带过了, 本文也算是一个补充.

既然是内容的梳理必然会牵涉到很多细节, 其中包括数学公式的推导, 这些在奥本海姆教授的两本著作《信号与系统》和《离散时间信号处理》都有详细推导过程. 本文的主要内容可以在《信号与系统》的第七章与《离散时间信号处理》的第四章中找到参考, 以下简写为《信-奥》与《离-奥》, 区别于参考郑君里教授的同名著作, 将简写作《信-郑》. 由于这部分采样内容在两本书中分布广泛、符号定义存在差异以及公式推导方式不一, 因此做一个总结是有必要的. 本文的一些内容会基于自己的理解, 可能错误在所难免, 不过书写是为了更好地理解.

在阅读这两本书的过程中, 令我十分敬佩的是作者清晰的写作思路. 如果把阅读一本书比作一次冒险旅行, 那么在旅途中作者不断地提醒你: 你现在身处何处？曾走过了哪些景点？经历了哪些岔路？我们这段路地主要景点是什么？我们旅行最终目的地又在何方？具体到某一知识点就是: 这个问题是怎么引入的？为什么要研究这个问题？这个问题在整个知识框架下是什么样的地位？搞清楚了这些再讲: 问题如何解决？解决方法怎么来的？为什么这么解决, 有什么好处？这个问题的解决会引入什么新问题？作者不厌其繁地讲这些也许会被一些人贴上“死于话多”的标签, 但我想对于初学者来说这总是好的, 国外的教材大抵有这样的特点.

扯远了, 这里也先给出本文的思路. 先梳理采样基础的内容, 包括对连续时间信号的采样和对离散时间信号（序列）的采样过程, 主要注意采样过程数学模型的建立. 接着由对离散时间信号的采样引出离散时间信号处理的两个操作—-抽取与内插, 再引出这两个操作的应用, 即实现重采样.

---

连续时间信号采样

采样过程主要关注采样过程的数学表述以及采样过程在时域与频域的变化, 这部分内容可参考《信-郑》P.156或《信-奥》P.109.

讨论连续时间采样时, 我们总是采用“理想采样过程”的叙述, 即是说采用周期冲激串来简化模拟采样过程, 这意味着将忽略单次采样的时间, 或者认为ADC的转化过程是瞬间完成的, 这在数学上是一种简化.

周期为T的采样周期冲激串表达式为:

$$P(t)=\sum^{\infty}_{n=-\infty}\delta(t-nT)$$

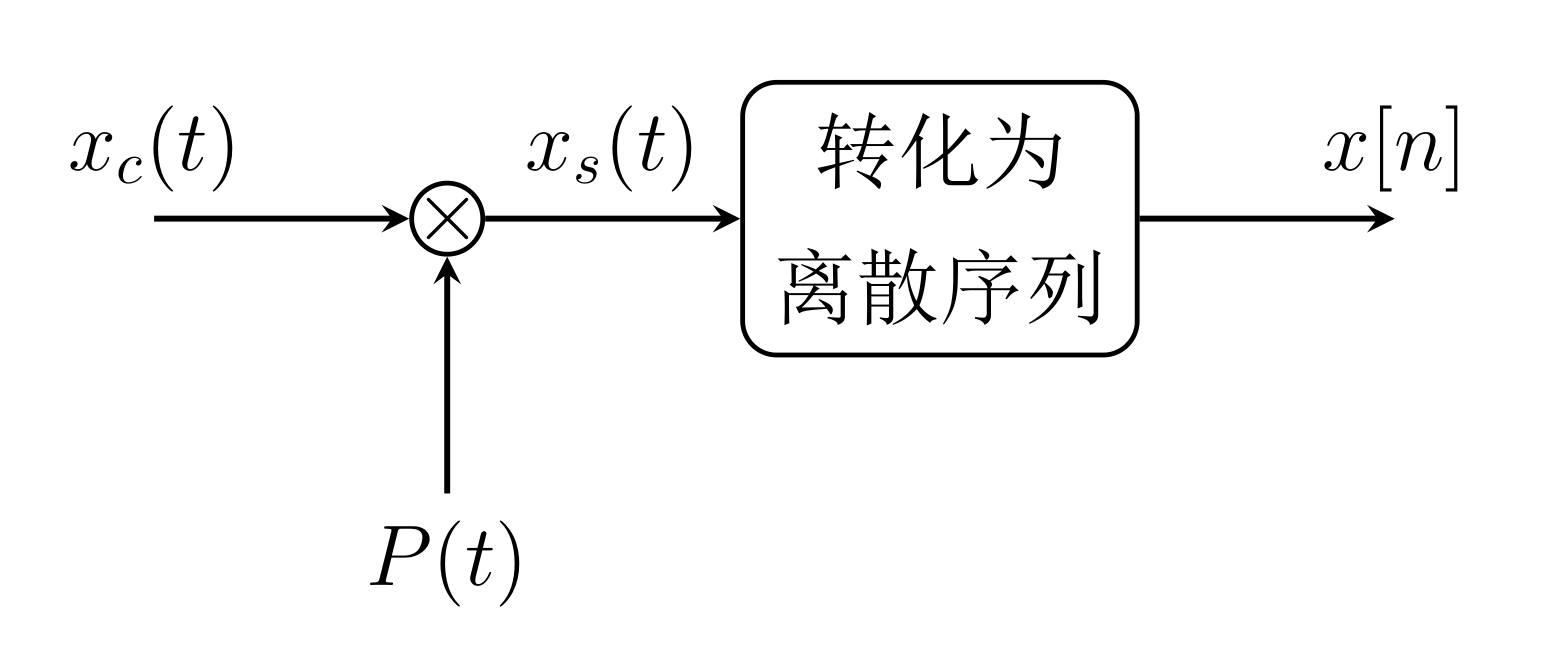
$x_{c}(t)$为被采样信号, $x_{s}(t)$为采样后信号, 整个采样过程由被采样信号与采样冲激串相乘来模拟, 即:

$$x_{s}(t)=x_{c}(t)P(t)=\sum^{\infty}_{n=-\infty}x_{c}(t)\delta(t-nT)=\sum^{\infty}_{n=-\infty}x_{c}(nT)\delta(t-nT)$$

以上即是理想采样过程的时域表达, 频域的分析有两种推导方法, 一种是借由傅里叶级数, 把冲激串傅里叶级数展开, 然后对$x_{c}(t)P(t)$做傅里叶变换；另一种是先利用周期函数傅里叶变换求冲激串的傅里叶变换, 然后借助傅里叶变换的相乘性质去求. 这里用第一种方法说明.

将$P(t)$用复指数形式傅里叶级数展开:

$$P(t)=\sum^{\infty}_{n=-\infty}\delta(t-nT)=\sum^{\infty}_{n=-\infty}a_{n}e^{jn\Omega_{s}t}$$

其中$a_{n}$为傅里叶级数系数, 而:

$$\Omega_{s}=\frac{2\pi}{T}=2\pi f_{s}$$

$\Omega_{s}$是连续时间的采样角频率, 连续时间的角频率用大写的$\Omega$表示, 而离散时间归一化后的角频率用小写$\omega$表示.

下面计算系数$a_{n}$:

$$\begin{align} a_{n} &= \frac{1}{T}\int^{T/2}_{-T/2}P(t)e^{-jn\Omega_{s}t}\mathrm{d}t \\ &= \frac{1}{T}\int^{T/2}_{-T/2}\left[\sum^{\infty}_{n=-\infty}\delta(t-nT)\right]e^{-jn\Omega_{s}t}\mathrm{d}t \\ &= \frac{1}{T}\int^{T/2}_{-T/2}\delta(t)e^{-j\cdot 0 \cdot \Omega_{s}t}\mathrm{d}t \\ &= \frac{1}{T} \end{align}$$

于是计算$x_{s}(t)$的傅里叶变换:

$$\begin{align*} X_{s}(j\Omega) = \mathscr{F}\left[x_{s}(t)\right] &= \mathscr{F}\left[x_{c}(t)\cdot P(t)\right] \\ &= \int^{+\infty}_{-\infty}x_{c}(t)P(t)e^{-j\Omega t}\mathrm{d}t \\ &= \int^{+\infty}_{-\infty}x_{c}(t) \left[\sum^{\infty}_{n=-\infty}\frac{1}{T}e^{jn\Omega_{s}t}\right]e^{-j\Omega t}\mathrm{d}t \\ &= \frac{1}{T}\sum^{\infty}_{n=-\infty}\int^{+\infty}_{-\infty}x_{c}(t)e^{-j(\Omega-n\Omega_{s})t}\mathrm{d}t \\ &= \frac{1}{T}\sum^{\infty}_{n=-\infty}X_{c}(j(\Omega-n\Omega_{s})) \end{align*}$$

可见采样之后频域变化是把$x_{c}(t)$的频域图像以$\Omega_{s}$进行周期延拓, 并且在幅度上乘因子$\frac{1}{T}$.

最后的说明, 在连续时间信号采样的数学表达中最后产生的是一个序列$x[n]$, 与$x_{c}(t)$有关系:

$$x[n]=x_{c}(nT)$$

实际上$x[n]$是$x_{s}(t)$把冲激替换为冲激能量的大小数值, 并在时间上做归一化处理得到的. 这部分的更详细的说明可参考《离-奥》P.109~110

也就是说整个采样过程应该是这样的:

---

离散时间信号采样

即对序列的采样过程, 参考《信-奥》的7.4节与《离-奥》P.127内容.

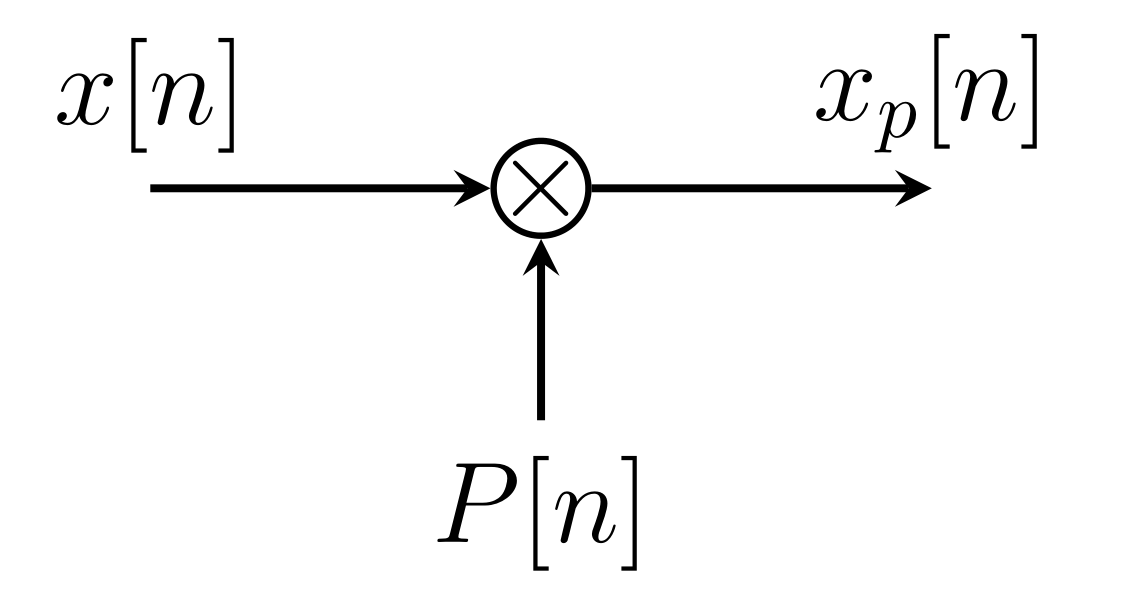
离散时间信号的采样过程的框图应该是这样的:

和连续时间采样一样, $x[n]$是待采样的序列, $P[n]$是用于采样的周期脉冲序列, $[n]$是一个周期脉冲序列, 周期为N（对应于连续时间的周期冲激串）, 而$x_{p}$是采样得到的序列, 有:

$$x_{p}[n]=x[n]\cdot P[n]=\sum^{\infty}_{k=-\infty}x[kN]\delta[n-kN]$$

另外在时域上n为N的整数倍的点上$x[n]$与$x_{p}[n]$值相同:

$$x_{p}[nN]=x[nN]$$

下面给出频域的分析, 由DTFT的相乘性质:

$$X_{p}(e^{j\omega})=\frac{1}{2\pi}\int_{2\pi}P(e^{j\theta})X(e^{j(\omega-\theta)})\mathrm{d}\theta$$

时域乘积频域做周期卷积, 这一性质可参考《信-奥》P.247, DTFT的相乘性质.

我们已知周期脉冲序列$P[n]$的DTFT:

$$P(e^{j\omega})=\frac{2\pi}{N}\sum^{\infty}_{k=-\infty}\delta(\omega-k\omega_{s}) \quad \quad\quad\omega_{s}=\frac{2\pi}{N}$$

上面的公式属于周期序列的DTFT, 所以引入了冲激函数, 这部分可参考《信-奥》P.236与《离-奥》P.443. 于是:

$$\begin{align*} X_{p}(e^{j\omega}) &= \frac{1}{2\pi}\int_{2\pi}P(e^{j\theta})X(e^{j(\omega-\theta)})\mathrm{d}\theta \\ &= \frac{1}{2\pi}\int_{2\pi} \left[ \frac{2\pi}{N}\sum^{\infty}_{k=-\infty}\delta(\theta-k\omega_{s})\right]X(e^{j(\omega-\theta)})\mathrm{d}\theta \\ &= \frac{1}{N}\sum^{\infty}_{k=-\infty}X(e^{j(\omega-k\omega_{s})})\int_{2\pi}\delta(\theta-k\frac{2\pi}{N})\mathrm{d}\theta \end{align*}$$

这式子稍微有点难理解, 这里是无穷项求和, 每一项中k是确定的, 且都包含后面的积分项, 这个积分项先选定$2\pi$长的积分区间, 只有当$k\frac{2\pi}{N}$落在这个积分区间内时积分值为1, 否则积分值为0. 对于$2\pi$长的积分区间最多有N个k值下积分值不为0, 至于是哪N个k值关系不大, 因为$X(e^{j(\omega-k\omega_{s})})$对k来说是以N为周期的, 于是只需取N个连续k值即可, 比如从0到N-1, 即:

$$X_{p}(e^{j\omega})=\frac{1}{N}\sum^{N-1}_{k=0}X(e^{j(\omega-k\omega_{s})}) \quad \quad\quad\omega_{s}=\frac{2\pi}{N}$$

如果把连续时间采样频域表达式拿过来做个对比:

$$X_{s}(j\Omega)=\frac{1}{T}\sum^{\infty}_{k=-\infty}X_{c}(j(\Omega-k\Omega_{s}))\quad \quad\quad\Omega_{s}=\frac{2\pi}{T}$$

就会发现两式形式差别不大, 采样过程在频域都是对原信号频谱做周期搬移. 而且离散采样得到的就是序列, 不用像连续时间采样那样需要最后转换为离散序列.

---

离散时间信号抽取与内插

在前一小节中得到的序列$x_{p}[n]$可以这样描述: 在n为N的整数倍的点上的值与$x[n]$相同, 其他n值点都是0, 为了节省存储空间, 需要对$x_{p}[n]$进行压缩, 这里所进行的操作就是“抽取”, 而其逆过程则称为“内插”.

同样要弄清楚做这两种处理时域与频域的变化及混叠情况, 这部分参考《信-奥》P.353与《离-奥》P.127.

设对$x_{p}[n]$抽取后得到的序列为$x_{b}[n]$, 于是在时域上有$x_{b}[n]=x_{p}[nN]$（$x_{b}[n]$直接由$x_{p}[n]$N整数倍的点组成）, 又因为之前有$x_{p}[nN]=x[nN]$, 故:

$$x_{b}[n]=x[nN]=x_{p}[nN]$$

然后寻找$x_{b}[n]$、$x_{p}[n]$与$x[n]$频域(DTFT)之间的关系, 推导过程可参考《信-奥》P.353~354.

首先$x_{b}[n]$的DTFT为:

$$X_{b}(e^{j\omega})=\sum^{\infty}_{k=-\infty}x_{b}[k]e^{-j\omega k}$$

再利用$x_{b}[n]$与$x_{p}[n]$的关系:

$$X_{b}(e^{j\omega})=\sum^{\infty}_{k=-\infty}x_{p}[kN]e^{-j\omega k}$$

做变量替换$n=kN$有$k=\frac{n}{N}$, 于是:

$$X_{b}(e^{j\omega})=\sum_{n=N \text{的整数倍}}x_{p}[n]e^{-j\omega \frac{n}{N}}$$

因为n不为N的整数倍时$x_{p}[n]=0$,故可写为:

$$X_{b}(e^{j\omega})=\sum^{\infty}_{n=-\infty}x_{p}[n]e^{-j\omega \frac{n}{N}}$$

把右边$\frac{n}{N}$看作整体, 右边即对$x_{p}[n]$的DTFT, 即:

$$X_{p}(e^{j\frac{\omega}{N}})=\sum^{\infty}_{n=-\infty}x_{p}[n]e^{-j\omega \frac{n}{N}}$$

联立得到:

$$X_{b}(e^{j\omega})=X_{p}(e^{j\frac{\omega}{N}})$$

之前由对序列采样, 我们已经得到了$x_{p}[n]$与$x[n]$的关系, 如下:

$$X_{p}(e^{j\omega})=\frac{1}{N}\sum^{N-1}_{k=0}X(e^{j(\omega-k\omega_{s})}) \quad \quad\quad\omega_{s}=\frac{2\pi}{N}$$

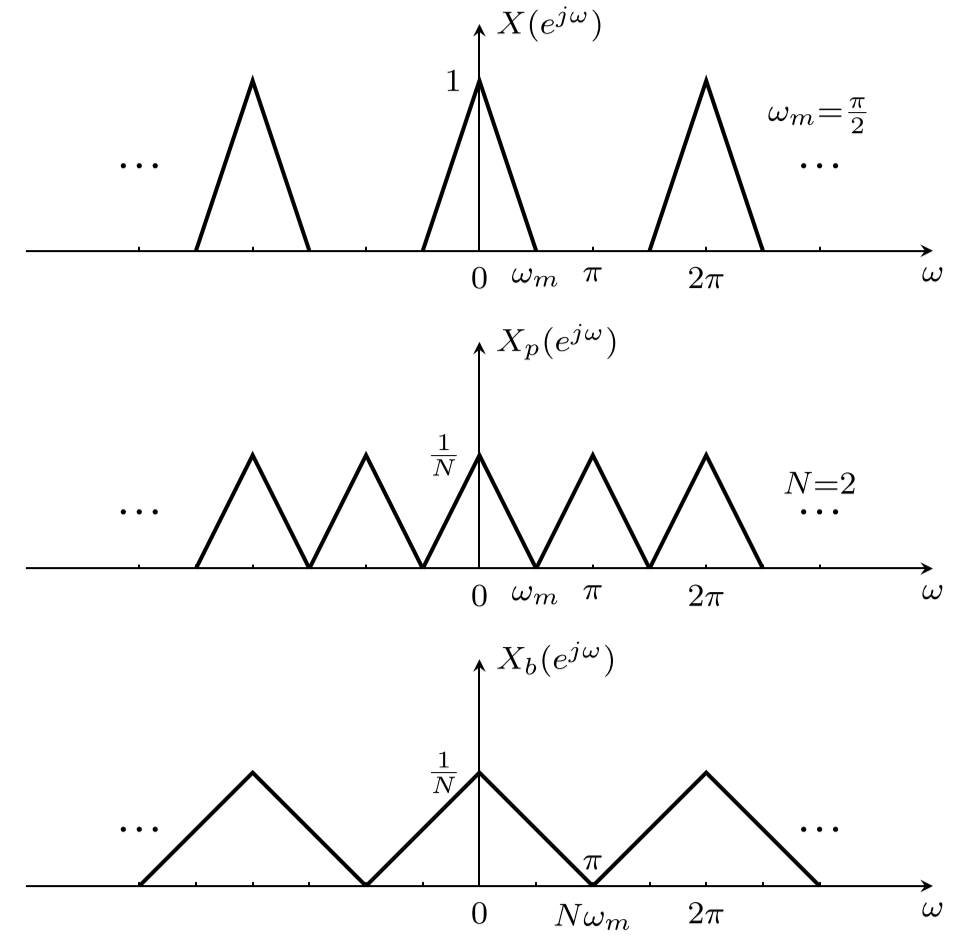
至此就得到了这三个序列的频域联系, 可见抽取将导致频域扩展. 如果再把上面两式联立得到:

$$X_{b}(e^{j\omega})=\frac{1}{N}\sum^{N-1}_{k=0}X(e^{j(\frac{\omega}{N}-k\omega_{s})}) \quad \quad\quad\omega_{s}=\frac{2\pi}{N}$$

上式后面会看到实际上就是采样率以N倍减小时得到的序列与原采样率下得到序列的频域关系.

下面是抽取在频域变化的例子:

下面是内插的说明, 内插是抽取的逆过程, 可以猜想频域变化为收缩. 参考《离-奥》P.131.

这里依旧设原序列为$x[n]$, 内插后序列为$x_{e}[n]$, 假设两者时域关系为:

$$x_{e}[n]= \begin{cases} x[\frac{n}{L}] & n=0,\pm L,\pm 2L,\dots\\ 0 & \text{others}.\\ \end{cases}$$

上式即以L为间隔的内插, 实际上就是在序列$x[n]$每两个值之间插入$(L-1)$个零值. 上式的一种等效写法为:

$$x_{e}[n]=\sum^{\infty}_{k=-\infty}x[k]\delta[n-kL]$$

这个式子可以这样理解: $x_{e}[n]$由无穷项相加构成, 只有当$n=kL$时, 那一项才不为0, 而是$x[\frac{n}{L}]$, 与之前的公式描述相同.

对$x_{e}[n]$做DTFT:

$$\begin{align*} X_{e}(e^{j\omega}) &= \sum^{\infty}_{n=-\infty} \left( \sum^{\infty}_{k=-\infty}x[k]\delta[n-kL]\right)e^{-j\omega n} \\ &= \sum^{\infty}_{k=-\infty}x[k] \left(\sum^{\infty}_{n=-\infty} \delta[n-kL]e^{-j\omega n} \right)\\ &= \sum^{\infty}_{k=-\infty}x[k] e^{-j\omega Lk} \\ &= X(e^{-j\omega L}) \end{align*}$$

由此便得到了$x_{e}[n]$与$x[n]$在频域的关系式.
上式推导过程中用到了:

$$\sum^{\infty}_{n=-\infty} \delta[n-kL]e^{-j\omega n}=e^{-j\omega Lk}$$

以上讨论了抽取与内插过程, 最后实现抽取的系统称为压缩器, 而实现内插的系统称为扩展器.

---

利用离散时间信号处理实现重采样

这个问题可以看作是之前讨论的抽取与内插的应用, 说的是运用这两种技术实现对原连续时间信号的采样率, 称之为重采样. 需要注意的是改变的是对连续时间信号采样率. 这其中涉及用抽取实现的减采样与用内插实现的增采样两部分.

之前讨论过对连续信号$x_{c}(t)$以周期T采样最终将得到序列$x[n]$, 他们之间的关系为:

$$x[n]=x_{c}(nT)$$

所谓“改变采样率”就是说换成周期为$T_{1}$去采样, 这样势必会得到一个新的采样序列记为$x_{1}[n]$, 有:

$$x_{1}[n]=x_{c}(nT_{1})$$

现在的问题是$x_{c}[n]$是未知的, $x[n]$已知, 而去求另一个采样率下对$x_{c}(t)$采样得到的序列$x_{1}[n]$, 解决问题的办法通常有两种, 一是先由$x[n]$重构出$x_{c}(t)$, 再调整以周期$T_{1}$重新进行采样得到$x_{1}[n]$, 另一种方法则通过$x[n]$与$x_{1}[n]$的关系, 用离散时间信号处理的方式求得$x_{1}[n]$, 这是这里得重点.

下面先讨论减采样. 我们的目的还是推导出原采样率下得到的序列与降低采样率后采样得到的序列频域上的关系.

在降低采样率的情况下, 讨论重新设定采样率为原采样率$\frac{1}{M}$的这种情况. 比如新采样周期$T_{d}$是原周期T的M倍:

$$T_{d}=MT$$

重采样得到的序列记作$x_{d}[n]$, 有:

$$x_{d}[n]=x_{c}(nT_{d})=x_{c}(nMT)$$

利用$x[n]=x_{c}(nT)$, 于是找到两采样序列之间的关系:

$$x_{d}[n]=x[nM]$$

这个时域关系之前刚讨论过, $x_{d}[n]$就是$x[n]$以M抽取得到的, 两者频域关系的表达式在抽取那里已经给出, 这里以M抽取, 故:

$$X_{d}(e^{j\omega})=\frac{1}{M}\sum^{M-1}_{k=0}X(e^{j(\frac{\omega}{M}-k\frac{2\pi}{M})})$$

此式完整的推导过程可参考《离-奥》P.128.

---

一个补充

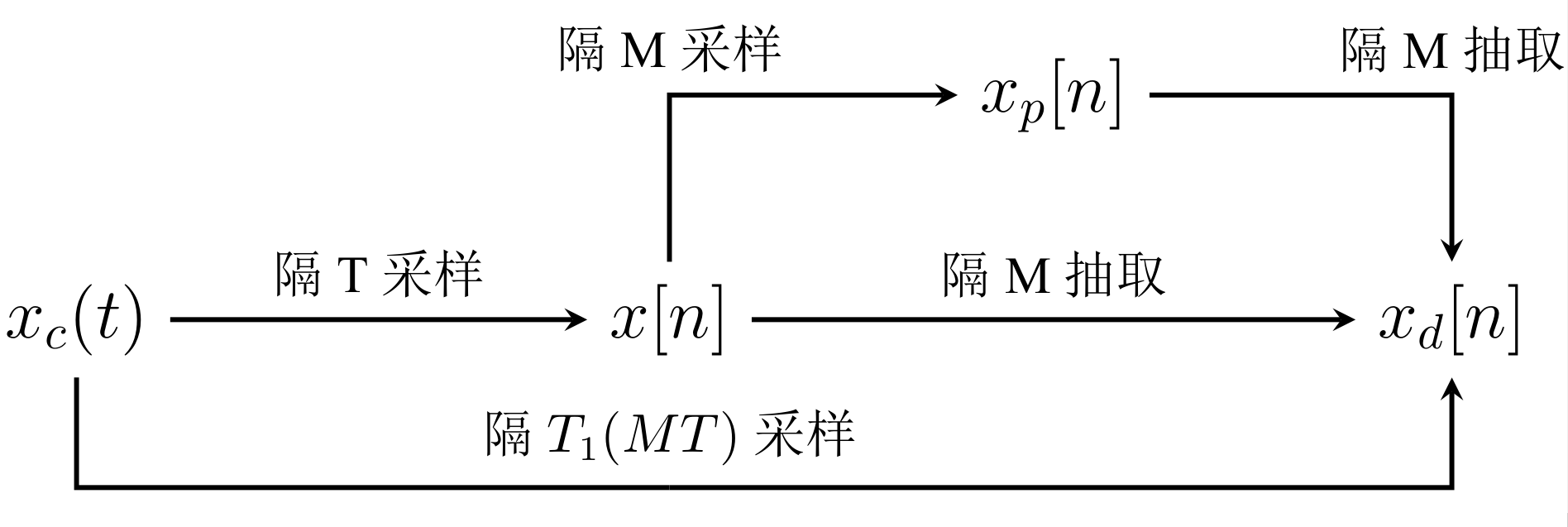
这里有一个之前一直没想通的地方, 就是之前讨论是这样一个过程:
$x[n]$是以周期为T对$x_{c}(t)$采样得到的, 然后是序列的采样过程, 假设采样周期为$N_{1}$, 得到$X_{p}[n]$. 最后对$x_{p}[n]$以比如$N_{2}$抽取, 得$x_{b}[n]$, 故这些序列在在频域得关系为:

$$X_{p}(e^{j\frac{\omega}{N_{1}}})=\sum^{\infty}_{n=-\infty}x_{p}[n]e^{-j\omega \frac{n}{N_{1}}}$$ $$X_{b}(e^{j\omega})=X_{p}(e^{j\frac{\omega}{N_{2}}})$$

联立得:

$$X_{b}(e^{j\omega})=\frac{1}{N_{1}}\sum^{N_{1}-1}_{k=0}X(e^{j(\frac{\omega}{N_{2}}-k\frac{2\pi}{N_{1}})})$$

这与前面$X_{d}(e^{j\omega})$对比, 会发现如果有$N_{1}=N_{2}=M$时, 两者完全相等. 这个等式成立是合理的, 事实上在推导的时候也是默认成立的, 不然就失去了意义.

另一点要注意的是对$x[n]$以N抽取与对$x_{p}[n]$以N抽取得到的序列相同, 都是$x_{b}[n]$, 因为抽取操作只关心n为N整数倍的那些点.

以上所有讨论的序列关系如下图:

---

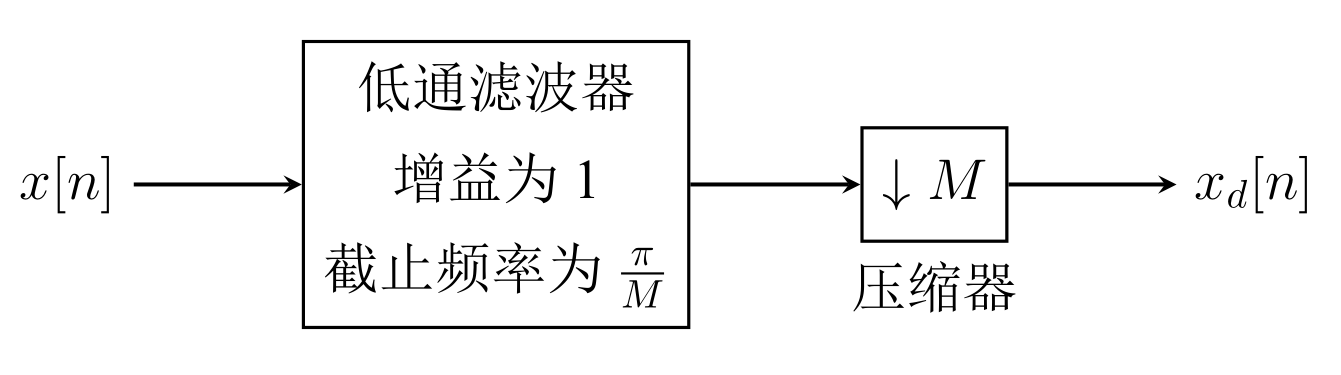
接下来是减采样系统的构成:

可见系统除了一个实现抽取操作的压缩器外还有个抗混叠滤波器, 这个滤波器的主要作用是把$x[n]$的频域截断到$\frac{\pi}{M}$, 因为进行以M为周期的抽取等效于对频域扩展M倍, 要不发生混叠, 压缩器输入信号带宽最大就是$\frac{\pi}{M}$.

同样对于增采样过程, 若以L倍增加采样率, 实际上可以通过对$x[n]$以L内插得到采样序列$x_{e}[n]$. 之前得到他们在频域上:

$$X_{e}(e^{j\omega})=X(e^{j\omega L})$$

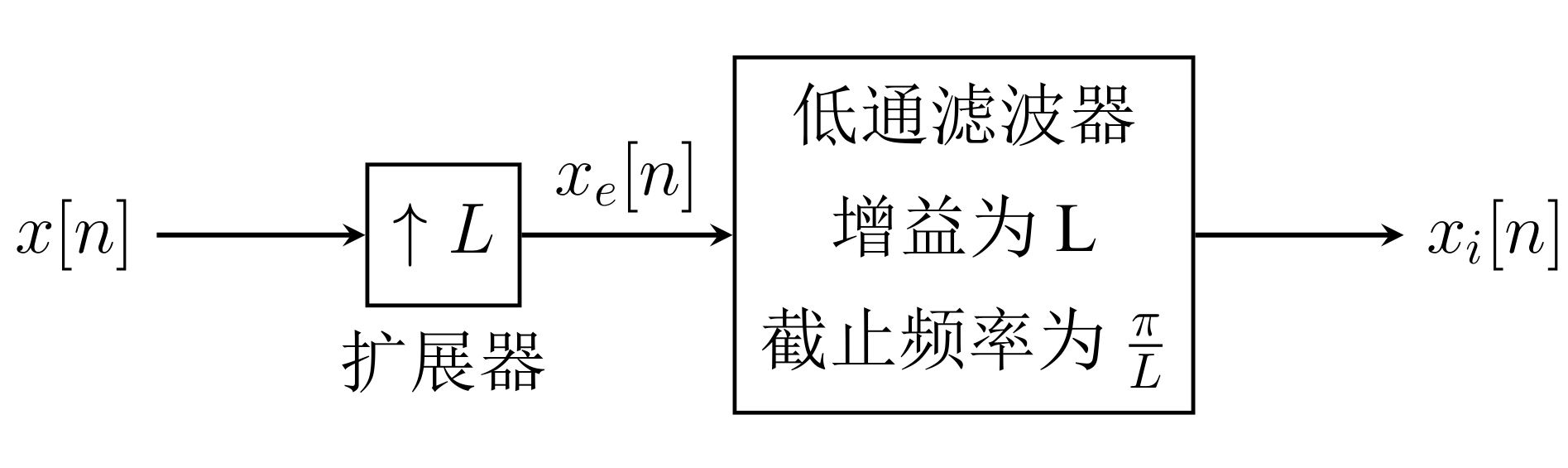
而增采样系统一般为:

可以看到除了一个实现内插的扩展器外还有一个低通滤波器, 这个低通滤波器是必须的.

一方面, 增益为L进行幅度调整, 对于以周期为T进行采样得到的序列$x[n]$, 在频域幅度是被采样信号的$\frac{1}{T}$, 故若将将采样周期改变为$\frac{T}{L}$, 应把幅度也调整为$\frac{L}{T}$, 而之前减采样过程的频域表达式中本身就会乘以因子$\frac{1}{M}$, 将$\frac{1}{T}$调整为$\frac{1}{MT}$, 因此不需要滤波器再对幅度进行调整.

另一方面经过$\frac{\pi}{L}$的低通滤波器后, 能滤除频谱多余部分, 使剩下来的部分以$2\pi$为周期.

---

小结

本文首先回顾了连续时间信号的采样过程与数学表达, 然后将采样的概念引到序列处理, 讨论了序列采样过程. 由于离散时间信号存取与处理特点, 引出序列的抽取与插值操作, 最后讨论利用抽取与插值实现改变采样率这一应用.

这里所讨论的采样都是时域的采样, 实际上在采样这块另一个重要的内容是对傅里叶变换的采样（频域的采样）, 特别在离散时间信号处理中对DTFT、DFT的采样, 这些内容对于理解另一类按频率抽取的FFT算法是必要的.
.
.
.
.
.
.
.
.
終わり