浅谈线性回归

之前学着用过线性回归的一些东西, 这里稍微整理下, 虽然是比较基础的内容, 希望能理出一个比较清晰的方法思路来, 如果能对到其他人理解这个问题有帮助那再好不过了:)

其实内容不多, 这里首先谈谈问题的背景引入回归这个概念, 以及他要解决的问题, 然后是今天的主角—线性回归方法, 从简单的一元函数开始说明, 再推广到实际应用上更一般的多元线性回归. 最小二乘法是最常用来解决线性问题的方法之一, 说穿了其实是一种参数估计方法, 是估计线性方程中的未知权向量$\boldsymbol{\beta}$的一种方法, 我们还会给出最小二乘法的矩阵运算形式, 这将便于我们编程来实现算法.

理论方面的内容主要参考了陈希孺教授的《概率论与数理统计》, 这是一本值得安利的教材, 难能可贵的是这书不是公式和定义堆砌而成的”工具书”, 作者更想传授的是一种统计学特有的思考方式. 同时也有参考其他讨论这个问题的资料, 比如也引入了一些统计学习语境下的观点与术语, 顺便统一了一下符号的表示方法.

回归分析

回归分析这是统计学应用的一个分支, 下面是从wiki百科上摘下来的解释:

回归分析(Regression Analysis)是一种统计学上分析数据的方法, 目的在于了解两个或多个变量间是否相关、相关方向与强度, 并建立数学模型以便观察特定变量来预测研究者感兴趣的变量. 更具体的来说, 回归分析可以帮助人们了解在只有一个自变量变化时因变量的变化量. 一般来说, 通过回归分析我们可以由给出的自变量估计因变量的条件期望.

回归可以理解为对于有相关性的变量, 通过建立数学模型(函数)去对变量之间的关系进行刻画的过程. 比如人的年龄与身高可能与体重存在某种相关性, 抽象出一个数学模型, 记$x^{(1)}$为一个的年龄, $x^{(2)}$为这个人的身高(之所以不用$x_{1}$与$x_{2}$是为了避免与之后的样本的右下标号弄混), 而$y$是体重, 这三个变量之间的相关性可能存在一个函数关系即:

$$y=f(x^{(1)},x^{(2)})+e$$

$e$是一种随机误差, 我们通常假设$e$是服从于均值为0, 方差为$\sigma^{2}$的正态分布.

回归分析的一个主要应用就是预测, 在这个例子里, 假如我们得到了这个$f$, 那么对于任何一个人, 只要报出他的年龄与身高就可以根据这个函数求出体重. 当然以上说的只是一种理想化, 事实上由于存在随机性与噪声, 我们永远也无法真正得到$y$, 再者与体重相关的变量因素可能不单单只有年龄与身高这么简单, 所以这种相关性的刻画是近似的, 而不是严格的. 我们只能估计得到$f$计算其函数值, 而希望$f$的值尽可能与$y$近似.

但是这个思路仍是有用的, 只是需要合理的处理变量与把误差尽可能限制在能够接受的范围内. 解决问题的关键往往不在消除误差, 而是使误差可控. 从上面的例子再抽象到一般, 假设我们认为有$p$个变量与$y$有关, 则可以表达为:

$$y=f(x^{(1)},x^{(2)},\dots,x^{(p)})+e$$

其中$f$被称为”回归函数”, 统计回归的目的就是去估计这个函数. 由于回归常用于预测问题, 故这里的$x^{(1)},x^{(2)},\dots,x^{(p)}$也被称为预测因子或预测量(predictors), 这是统计学中术语, 在应用中也称为特征(features), 这在模式识别(PR, Pattern Recognition)问题中更为常用.

为了去估计$f$, 样本是必要的, 样本(sample)是采样得到的一组组数据, 或者说是观测值(observation) 每一个样本都包含了$p$个变量与$y$的值, 样本中蕴藏着这个模型(或者说函数$f$)的信息. 从统计机器学习的角度看回归是一种监督学习(supervised learning), 从样本信息中”学习”得到我们需要的模型.

以上我们一直在说模型, 函数, 那么我们对于$f$究竟有多少了解? 根据不同了解情况, 可以简单地把回归分成两类, 若对$f$没有任何的了解, 无法给出$f$数学形式的任何假定(assumption), 这种情况称”无参数回归”, 不做讨论; 另一种则更常用, 即先假定了$f$的数学形式, 只是这个函数或者说模型中存在一些尚未确定的参数, 这些参数影响着$f$的性态, 此时求解回归问题的更具体地说, 即是通过样本或者说观测值, 去估计这些未知参数, 即熟悉的参数估计问题(点估计或区间估计), 这也称为”参数回归”. 下面要说到的线性回归即是假定$f$为线性函数所进行的参数回归, 之所以重视这种情况, 是因为这是应用上最广泛, 理论发展最完善的特例之一.

既然是参数估计问题就离不开采样. 假设有$N$个样本, 记为${(\boldsymbol{x}_{1},y_{1}),(\boldsymbol{x}_{2},y_{2}),\dots,(\boldsymbol{x}_{N},y_{N})}$:

$$\boldsymbol{x_{i}}= \begin{bmatrix} x_{i}^{(1)} \\ x_{i}^{(2)} \\ \vdots \\ x_{i}^{(p)} \\ \end{bmatrix}_{p\times1}$$ $$y_{i}=f(\boldsymbol{x_{i}})+e_{i}\qquad i=1,2,\dots,N$$

可以用矩阵简洁地表达为:

$$\boldsymbol{y}=f(\boldsymbol{X})+\boldsymbol{e}$$

其中:

$$\boldsymbol{y}= \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{N} \\ \end{bmatrix}_{N\times1}$$ $$\boldsymbol{X}= \begin{bmatrix} \boldsymbol{x}_{1}^{T} \\ \boldsymbol{x}_{2}^{T} \\ \vdots \\ \boldsymbol{x}_{N}^{T} \\ \end{bmatrix}_{N\times p}$$ $$\boldsymbol{e}= \begin{bmatrix} e_{1} \\ e_{2} \\ \vdots \\ e_{N} \\ \end{bmatrix}_{N\times1}$$

线性回归

就像之前说的, 线性回归是假定$f$为线性方程所进行的参数回归. 所谓”线性方程”, 是指$f$有如下形式:

$$f(x^{(1)},x^{(2)},\dots,x^{(p)})=b_{0}+b_{1}x^{(1)}+b_{2}x^{(2)}+\dots+b_{p}x^{(p)}$$

然后采样$N$次, 对于第$i$次采样得到

$$y_{i}=b_{0}+b_{1}x_{i}^{(1)}+b_{2}x_{i}^{(2)}+\dots+b_{p}x_{i}^{(p)}+e_{i}\qquad i=1,2,\dots,N$$

这里有一个问题需要先说明, 我们通常需要对采样得到的数据进行”中心化”, 具体操作为把上式改写为:

$$y_{i}=\beta_{0}+\beta_{1}z_{i}^{(1)}+\beta_{2}z_{i}^{(2)}+\dots+\beta_{p}z_{i}^{(p)}+e_{i}\qquad i=1,2,\dots,N$$

可以求得:

$$z^{(k)}_{i}=x_{i}^{(k)}-\bar{x}^{(k)}\qquad i=1,2,\dots,N;k=1,2,\dots,p$$ $$\bar{x}^{(k)}=\frac{1}{N}\sum^{N}_{i=1}x^{(k)}_{i}\qquad k=1,2,\dots,p$$ $$\beta_{k}=b_{k}\qquad k=1,2,\dots,p$$ $$\beta_{0}=b_{0}+b_{1}\bar{x}^{(1)}+\dots+b_{p}\bar{x}^{(p)}$$

“中心化”后需要估计的参数由$b_{k}$转变为$\beta_{k}$, 这样处理地好处是相比估计得到的$\hat{b}_{k}$, 各$\hat{\beta}_{k}$之间是互不相关的. 这体现了”中心化”处理的优势.

另外我们注意到, “中心化”后:

$$\sum^{N}_{i=1}z^{(k)}_{i}=\sum^{N}_{i=1}\left(x_{i}^{(k)}-\bar{x}^{(k)}\right)=\sum^{N}_{i=1}x_{i}^{(k)}-N\bar{x}^{(k)}=0$$

“中心化”或者说是模型的”中心化”, 实际上可以理解为是对样本的预处理过程, 我们一般假定这个预处理过程是事先完成的, $z^{(k)}_{i}$仍然用$x^{(k)}_{i}$来表示(但是知道此时的样本已经经过”中心化”处理了). 于是我们的方程描述成:

$$y_{i}=\beta_{0}+\beta_{1}x_{i}^{(1)}+\beta_{2}x_{i}^{(2)}+\dots+\beta_{p}x_{i}^{(p)}+e_{i}\qquad i=1,2,\dots,N$$

同时有:

$$\sum^{N}_{i=1}x^{(k)}_{i}=0\qquad k=1,2,\dots,p$$

可以看到$x^{(k)}_{i}$通过$\beta_{k}$进行线性加权. $\beta_{k}$即是每一个对应预测因子的权重. $\beta_{0}$这一项是孤立的常数项, 有时称这项为线性方程的截距(intercept). 下面依然试图用矩阵来简化线性方程的描述.

为了表示方便一般把上式写成两向量内积(inner product)的形式:

$$y=\beta_{0}+\boldsymbol{x}^{T}\boldsymbol{\beta}+e$$

这里$\boldsymbol{\beta}$与$\boldsymbol{x}$都是列向量:

$$\boldsymbol{\beta}= \begin{bmatrix} \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{p} \\ \end{bmatrix}_{p\times1}$$ $$\boldsymbol{x}= \begin{bmatrix} x^{(1)} \\ x^{(2)} \\ \vdots \\ x^{(p)} \\ \end{bmatrix}_{p\times1}$$

为了运算的便利, 有时也把$\boldsymbol{x}$扩一维, 添加$x^{(0)}=1$, 这样再把$\beta_{0}$加入$\boldsymbol{\beta}$, 就得到形式更为简洁的:

$$y=\boldsymbol{x}^{T}\boldsymbol{\beta}+e$$

这里$\boldsymbol{x}$与$\boldsymbol{\beta}$列向量都是$p+1$维的, 称此线性回归问题为p元的的线性回归问题, 因为有p个预测因子. 向量$\boldsymbol{\beta}$也称之为权向量, 权向量的取值空间称为权空间(weight space)

然后$N$次采样后:

$$\boldsymbol{y}=\boldsymbol{X}\boldsymbol{\beta}+\boldsymbol{e}$$ $$\boldsymbol{X}= \begin{bmatrix} \boldsymbol{x}_{1}^{T} \\ \boldsymbol{x}_{2}^{T} \\ \vdots \\ \boldsymbol{x}_{N}^{T} \\ \end{bmatrix}_{N\times (p\times 1)}$$

一元线性回归

所有的准备都已完毕, 下面来解这个问题, 即如何估计得到权向量.

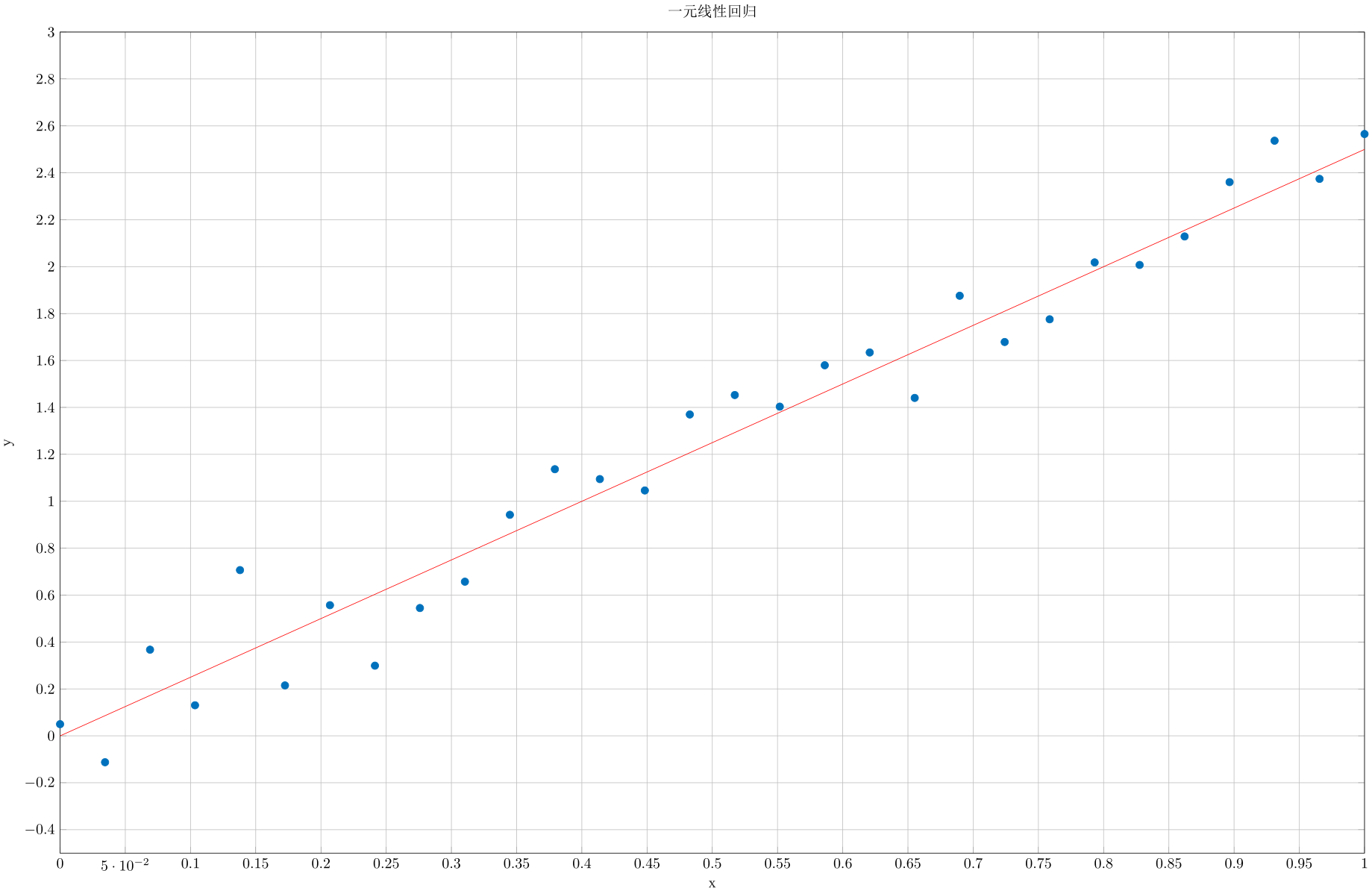
对于一元与二元线性回归我们有非常直观的解释, 下面讨论一元线性回归, 其模型假设为:

$$y=\beta_{0}+\beta_{1}x+e$$

对于$N$次采样我们画出图来:

图中的点即样本, 我们需要找到一种方法, 在某个标准下, 找到能比较准确描述输入输出关系的那条线, 比如图中的红线.

这条红线便是预测线, 他由如下线性方程描述:

$$\hat{y}=\hat{\beta}_{0}+\hat{\beta}_{1}x$$

$\hat{\beta}_{0}$与$\hat{\beta}_{1}$是对$\beta_{0}$与$\beta_{1}$的估计, 如何获得这个估计?我们需要选择一个策略, 即一个衡量模型好坏的标准. 一个直观的办法就是看模型预测出的的$\hat{y}$在那些样本点上与采样值$y$的差距, 我们取:

$$L(\hat{\beta}_{0}, \hat{\beta}_{1})=\sum^{N}_{i=1}(y_{i}-\hat{y}_{i})^{2}$$

上式直观的解释是: 我们所寻找的预测线(模型), 应该使所有样本点到预测线竖直距离和最小. 这就是最小二乘法(Least Squares)在一元情况下遵循的策略. 同时也知道了, 最小二乘法属于一种点估计.

在统计学习中上式也被称为损失函数(loss function), 更确切地说是一种平方损失函数(quadratic loss function). 损失函数值越小(通过调节参数$\hat{\beta}_{0},\hat{\beta}_{1}$大小)模型越好.

在统计学中, 曾定义残差平方和(RSS,residual sum of squares), 其计算公式与$L(\hat{\beta}_{0}, \hat{\beta}_{1})$相同, 所以也可以认为最小二乘法是求得RSS最小的权向量估计.

利用多元函数求极值的方法, 我们很容易就可以求得这个问题的解析解.

$$L(\hat{\beta}_{0}, \hat{\beta}_{1})=\sum^{N}_{i=1}(y_{i}-\hat{y}_{i})^{2}=\sum^{N}_{i=1}(y_{i}-\hat{\beta}_{0}- \hat{\beta}_{1}x_{i})^{2}$$

上式分别对$\hat{\beta}_{0}, \hat{\beta}_{1}$求偏导, 并令其为0. 得:

$$\dfrac{\partial L}{\partial \hat{\beta}_{0}}=-2\sum^{N}_{i=1}[y_{i}-\hat{\beta}_{0}- \hat{\beta}_{1}x_{i}]=0$$ $$\dfrac{\partial L}{\partial \hat{\beta}_{1}}=-2\sum^{N}_{i=1}x_{i}[y_{i}-\hat{\beta}_{0}- \hat{\beta}_{1}x_{i}]=0$$

由于经过”中心化”, 之前说过有结论:

$$\sum^{N}_{i=1}x^{(k)}_{i}=0\qquad k=1,2,\dots,p$$

于是可解出$\hat{\beta}_{0},\hat{\beta}_{1}$:

$$\hat{\beta}_{0}=\bar{y}=\frac{1}{N}\sum^{N}_{i=1}y_{i}$$ $$\hat{\beta}_{1}=\frac{\sum\limits^{N}_{i=1}x_{i}y_{i}}{\sum\limits^{N}_{i=1}x^{2}_{i}}$$

$\hat{\beta}_{0},\hat{\beta}_{1}$本身有一些比较好的性质, 比如可以证明他们是$\beta_{0},\beta_{1}$的无偏估计, 并且他们是不相关的. 当假设随机误差$e$服从正态分布时, 他们还是独立的, 并且是$\beta_{0},\beta_{1}$的最小方差无偏估计, 证明可参考《概率论与数理统计》P.267~269内容.

多元线性回归

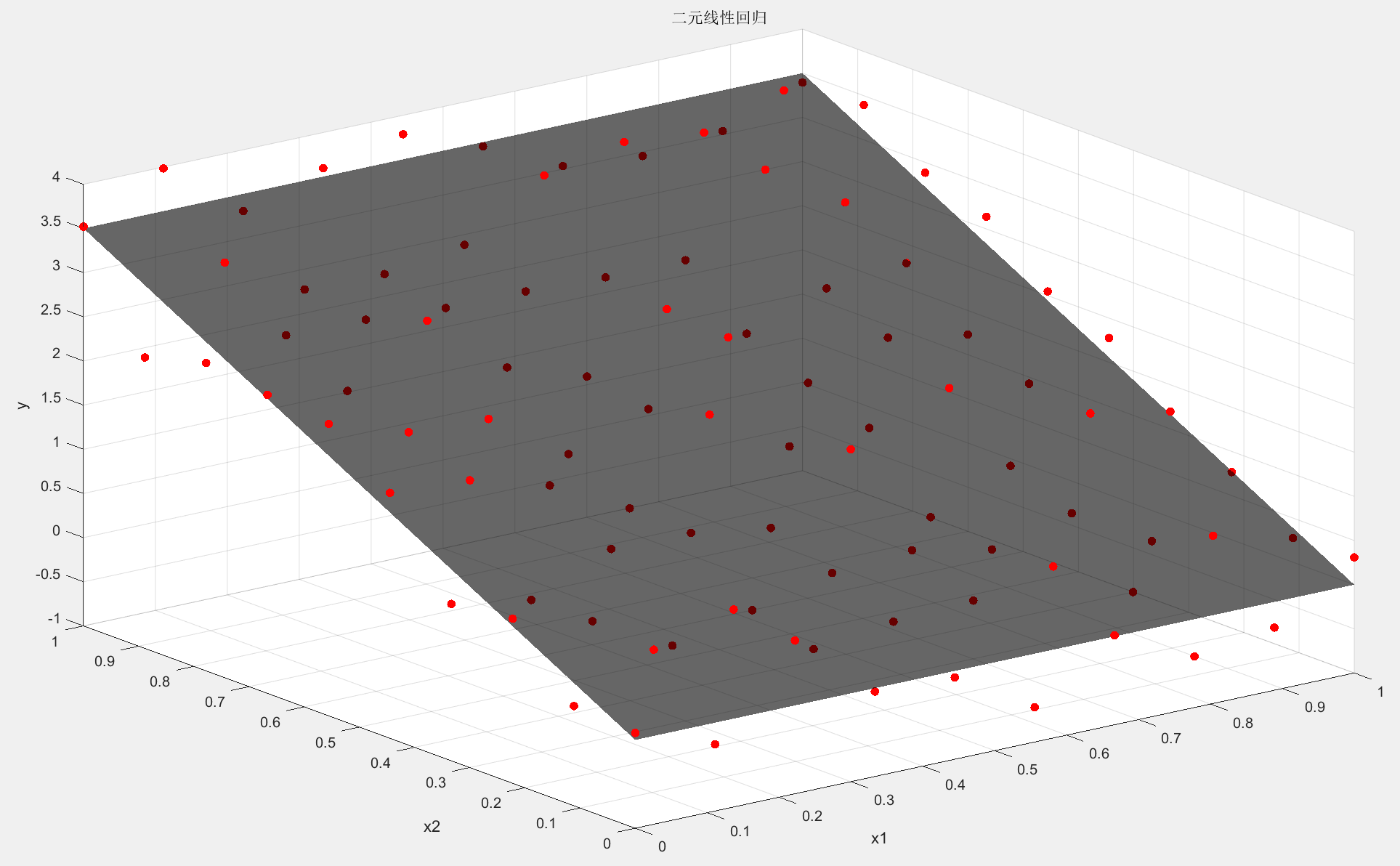
当$p=2$时即二元线性回归, 我们仍然可以直观地想象模型:

此时对于每个样本点有两个特征$\boldsymbol{x}_{i}=(x^{(1)}_{i},x^{(2)}_{i})$, 故模型是一个空间平面去拟合(fit)样本. 此时最小二乘法求解的原则是样本点到平面竖直距离和最小.

$p>2$的多元线性回归就没有这么直观了, 但我们依然可以知道模型是使用超平面(hyperplane)去拟合样本.

为了能直接推导出最后实用的矩阵运算方法, 我们对$\boldsymbol{x}_{i}$升1维处理, 正如之前说过的, 令$x^{(0)}_{i}=1$, 于是:

$$y_{i}=\hat{\beta}_{0}x^{(0)}_{i}+\hat{\beta}_{1}x_{i}^{(1)}+\hat{\beta}_{2}x_{i}^{(2)}+\dots+\hat{\beta}_{p}x_{i}^{(p)}\qquad i=1,2,\dots,N$$

推导权向量的估计与一元时类似, 损失函数为:

$$L(\hat{\beta}_{0},\hat{\beta}_{1},\dots,\hat{\beta}_{p})=\sum^{N}_{i=1}(y_{i}-\hat{y_{i}})^{2}=\sum^{N}_{i=1}(y_{i}-\hat{\beta}_{0}x^{(0)}_{i}-\hat{\beta}_{1}x_{i}^{(1)}-\hat{\beta}_{2}x_{i}^{(2)}-\dots-\hat{\beta}_{p}x_{i}^{(p)})^{2}$$

对各权向量求导令其为0:

$$\dfrac{\partial L}{\partial \hat{\beta}_{0}}=0,\quad \dfrac{\partial L}{\partial \hat{\beta}_{1}}=0,\quad \dfrac{\partial L}{\partial \hat{\beta}_{2}}=0,\quad\dots,\quad \dfrac{\partial L}{\partial \hat{\beta}_{p}}=0$$

由于样本经过”中心化”处理, 依然有:

$$\sum^{N}_{i=1}x^{(k)}_{i}=0\qquad k=1,2,\dots,p$$

对于$\hat{\beta}_{0}$的偏导, 可以整理为:

$$\dfrac{\partial L}{\partial \hat{\beta}_{0}} = -2\sum^{N}_{i=1}\left( y_{i}-\hat{\beta}_{0}x^{(0)}_{i}-\hat{\beta}_{1}x^{(1)}_{i}-\dots-\hat{\beta}_{p}x^{(p)}_{i}\right)=0$$ $$\sum^{N}_{i=1}x^{(0)}_{i}y_{i}=\hat{\beta}_{0}\sum^{N}_{i=1}x^{(0)}_{i}x^{(0)}_{i}+\hat{\beta}_{1}\sum^{N}_{i=1}x^{(0)}_{i}x^{(1)}_{i}+\dots+\hat{\beta}_{p}\sum^{N}_{i=1}x^{(0)}_{i}x^{(p)}_{i}$$

把剩余方程相同处理列在一起:

$$\begin{cases} \hat{\beta}_{0}\sum^{N}_{i=1}x^{(0)}_{i}x^{(0)}_{i}+\hat{\beta}_{1}\sum^{N}_{i=1}x^{(0)}_{i}x^{(1)}_{i}+\dots+\hat{\beta}_{p}\sum^{N}_{i=1}x^{(0)}_{i}x^{(p)}_{i}=\sum^{N}_{i=1}x^{(0)}_{i}y_{i} \\ \hat{\beta}_{0}\sum^{N}_{i=1}x^{(1)}_{i}x^{(0)}_{i}+\hat{\beta}_{1}\sum^{N}_{i=1}x^{(1)}_{i}x^{(1)}_{i}+\dots+\hat{\beta}_{p}\sum^{N}_{i=1}x^{(1)}_{i}x^{(p)}_{i}=\sum^{N}_{i=1}x^{(1)}_{i}y_{i} \\ \vdots \\ \hat{\beta}_{0}\sum^{N}_{i=1}x^{(p)}_{i}x^{(0)}_{i}+\hat{\beta}_{1}\sum^{N}_{i=1}x^{(p)}_{i}x^{(1)}_{i}+\dots+\hat{\beta}_{p}\sum^{N}_{i=1}x^{(p)}_{i}x^{(p)}_{i}=\sum^{N}_{i=1}x^{(p)}_{i}y_{i} \end{cases}$$

下面用矩阵对上式进行形式上的简化, 令:

$$\boldsymbol{X}= \begin{bmatrix} x^{(0)}_{1} & x^{(1)}_{1} & \ldots & x^{(p)}_{1} \\ x^{(0)}_{2} & x^{(1)}_{2} & \ldots & x^{(p)}_{2} \\ \vdots & \vdots\ & \ddots & \vdots \\ x^{(0)}_{N} & x^{(1)}_{N} & \ldots & x^{(p)}_{N} \\ \end{bmatrix}= \begin{bmatrix} \boldsymbol{x}_{1}^{T} \\ \boldsymbol{x}_{2}^{T} \\ \vdots \\ \boldsymbol{x}_{N}^{T} \\ \end{bmatrix}_{N\times (p+1)}$$ $$\boldsymbol{y}= \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{N} \\ \end{bmatrix}_{N\times1}$$ $$\boldsymbol{\hat{\beta}}= \begin{bmatrix} \beta_{0} \\ \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{p} \\ \end{bmatrix}_{(p+1)\times1}$$

于是上式可简化为:

$$\boldsymbol{X}^{T}\boldsymbol{X}\boldsymbol{\hat{\beta}}=\boldsymbol{X}^{T}\boldsymbol{y}$$

当$\boldsymbol{X}^{T}\boldsymbol{X}$可逆, 有:

$$\boldsymbol{\hat{\beta}}=(\boldsymbol{X}^{T}\boldsymbol{X})^{-1}\boldsymbol{X}^{T}\boldsymbol{y}$$

最小二乘法矩阵表示的简单推导

利用矩阵代数中的向量的数量函数对向量的导数的概念, 上述推导过程会更加简洁. 直接从损失函数出发:

$$L(\hat{\boldsymbol{\beta}})=\sum^{N}_{i=1}(y_{i}-\boldsymbol{x}_{i}^{T}\hat{\boldsymbol{\beta}})^{2}= \begin{bmatrix} y_{1}-\boldsymbol{x}_{1}^{T}\boldsymbol{\hat{\beta}} \\ y_{2}-\boldsymbol{x}_{2}^{T}\boldsymbol{\hat{\beta}} \\ \vdots \\ y_{N}-\boldsymbol{x}_{N}^{T}\boldsymbol{\hat{\beta}} \\ \end{bmatrix}^{T} \begin{bmatrix} y_{1}-\boldsymbol{x}_{1}^{T}\boldsymbol{\hat{\beta}} \\ y_{2}-\boldsymbol{x}_{2}^{T}\boldsymbol{\hat{\beta}} \\ \vdots \\ y_{N}-\boldsymbol{x}_{N}^{T}\boldsymbol{\hat{\beta}} \\ \end{bmatrix}= (\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\hat{\beta}})^{T}(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\hat{\beta}})$$ $$\mathrm{d}L=-(\boldsymbol{X}\mathrm{d}\boldsymbol{\hat{\beta}})^{T}(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\hat{\beta}})-(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\hat{\beta}})^{T}\boldsymbol{X}\mathrm{d}\boldsymbol{\hat{\beta}}$$

再利用迹技巧(trace trick), 可以得到:

$$\mathrm{d}L=-2(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\hat{\beta}})^{T}\boldsymbol{X}\mathrm{d}\boldsymbol{\hat{\beta}}$$

故:

$$\frac{\mathrm{d}L}{\mathrm{d}\boldsymbol{\hat{\beta}}}=-2(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\hat{\beta}})^{T}\boldsymbol{X}=-2\boldsymbol{X}^{T}(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\hat{\beta}})=0$$ $$\boldsymbol{X}^{T}\boldsymbol{y}-\boldsymbol{X}^{T}\boldsymbol{X}\boldsymbol{\hat{\beta}}=0$$

同样解得:

$$\boldsymbol{\hat{\beta}}=(\boldsymbol{X}^{T}\boldsymbol{X})^{-1}\boldsymbol{X}^{T}\boldsymbol{y}$$

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
終わり