FFT 为什么那么快

17年第一篇文章´_ゝ｀
其实这篇文章早之前已经完成了大部分, 谈谈自己对FFT的理解, 碍于种种原因没有发. 期间本站也崩过一次, 还是免费域名, 从tk换到了ml, 又能继续折腾了.

FFT或者说快速傅里叶变换算法是一类高效计算离散傅里叶变换的方法, 现在已经被广泛地应用于数字
信号处理系统中了, 对比前面讨论过的直接计算或者Goertzel算法都需要相当于正比于$N^{2}$的浮点运算量, 而FFT是一种正比于$N\log_{2}N$的离散傅里叶变换计算方法, 而且当N值越大, 这种计算方法的优势就越明显. 画了幅图可以感受下.

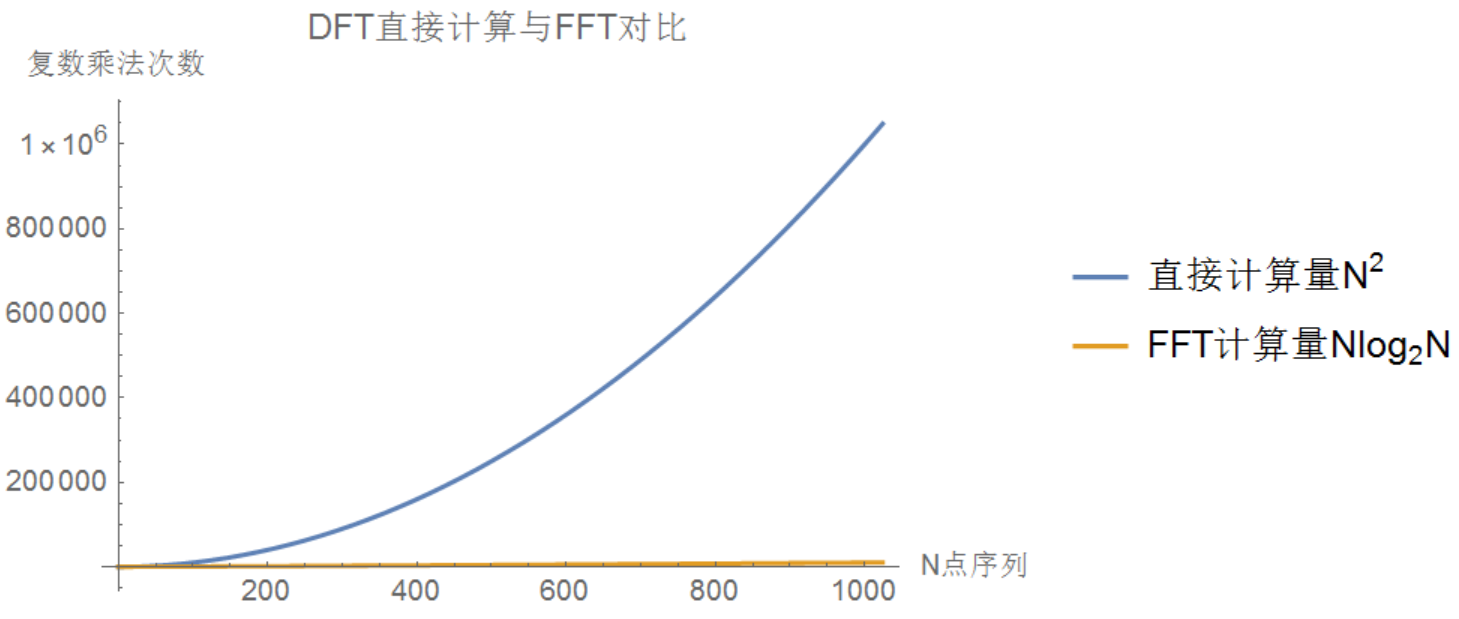
FFT是一类蝶形计算, 计算方式不复杂, 但要弄懂它的来龙去脉, 还是得费点功夫, 这也是我迟迟没下笔的原因之一. 这里重新理了下FFT的实现思路, 谈谈自己的理解, 同时希望对于这类算法能有触类旁通的益处.

FFT算法按大类分成时间抽取与频率抽取的两种类型. 然后根据计算序列样值点个数可以分为一系列以n为基的计算方案, 这里重点讨论以2为基的计算过程, 也就是样值点$N=2^{n}$, 从中能方便快速的领悟FFT计算的原理. 至于处理更一般的情况, 一种方法是把N拆分成比如两个或更多的2的幂次个点的序列, 将N个点的DFT变成几组点DFT的和, 然后利用以2为基的FFT计算过程.

OK, 这里重点讨论按时间抽取的FFT算法并且以2为基这种特殊的情况作为切入点. 之前说了FFT本质上也是一种DFT的简化算法, 其大致思路是把序列拆成两个子序列, 分别计算它们的DFT, 我们会发现此时的运算量比直接计算已经有所减少. 当序列比较长时, 很自然我们仍然可以对两个子序列进行拆分变成更短的序列, 从而进一步减少计算量. 事实上当长度为$2^{n}$个样值点时, 我们最多能够拆到2个长度为1的序列进行DFT, 此时可预见计算整个序列的DFT的运算量将达到最小.

思路简单粗暴, 下面将先讨论FFT如何将序列拆分, 并使得这种操作能够不断重复进行直至简化到两个样值点进行DFT. 好吧, 其实也没那么复杂, 这里既然以2为基的FFT为例, 每次把序列拆成奇序列和偶序列就行了. 这可以通过改变离散时间信号采样率这一方式实现, 也就是抽取和内插操作. 来看下图:

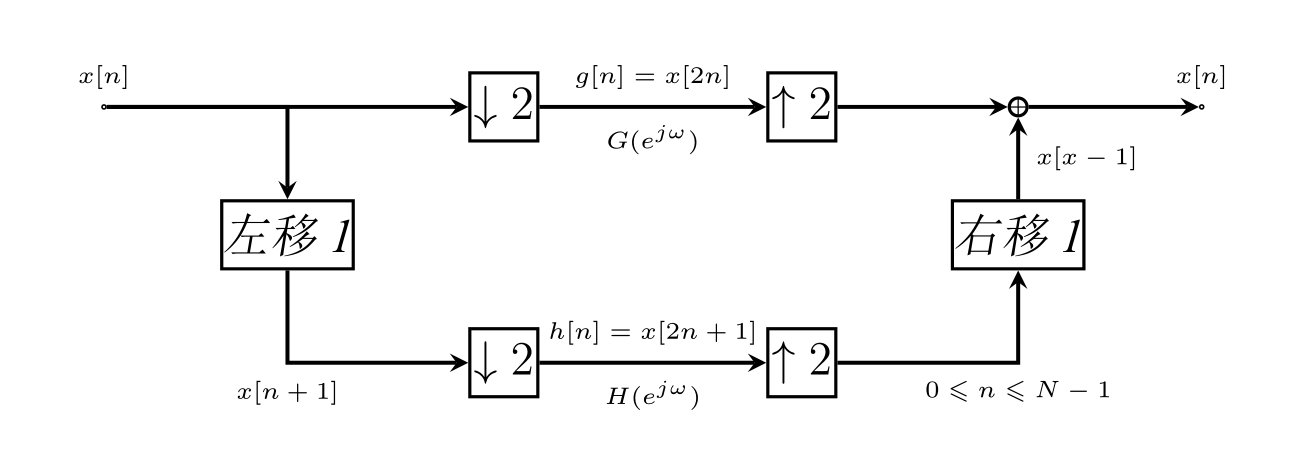
别看上图好像什么也没干（我一开始也这么想的）, 但仔细琢磨就会发现它很好地说明了FFT在时域和频域的拆分操作. 在说明之前需要承认的是上述操作在时域是正确的, 也就是$x[n]$经过上述操作最终又回到$x[n]$是能够实现的（借由提取和内插操作的时域变化可看出）, 其次, 上图中的左移右移实际上应该是序列的循环左移与循环右移.

先来看上图的左边部分, 通过压缩器提取得到的$g[n]$与$h[n]$便是FFT中经过一次拆分得到的子序列. 不难看出$g[n]=x[2n]$提取的是$x[n]$的位置序号为偶数的点, 而$h[n]=x[2n+1]$提取的是$x[n]$位置序号为奇数的点.

此时我们不妨回忆一下重采样, 以便得到采样前后的频域变化. 回（bai）忆（du）中…

$$X_{d}(e^{j\omega})=\frac{1}{M} \sum\limits_{i=0}^{M-1}X(e^{j(\omega/M-2\pi i/M)})$$

在这里的M就等于2, 于是有:

$$G(e^{j\omega})=\frac{1}{2}(X(e^{j\omega/2})+X(e^{j(\omega-2\pi)/2}))$$ $$H(e^{j\omega})=\frac{1}{2}(X(e^{j\omega/2})e^{j\omega/2}+X(e^{j(\omega-2\pi)/2})e^{j(\omega-2\pi)/2})$$

注意$H(e^{j\omega})$的表达式, 由于到$h[n]$有一个左移操作, 由DTFT性质知在频域需乘因子$e^{j\omega}$.

唔, 如果可能的话, 我们还是比较希望用$G(e^{j\omega})$与$H(e^{j\omega})$来表示$X(e^{j\omega})$, 这样就能直观地看出子序列单独进行DFT后经过怎样的组合变成整个序列的DFT的, 这才是我们关心的问题.

此时图右边的频域分析可以很快看出这一点, 只需要再回（bai）忆（du）一下经过增采样前后频域变化就行了:

$$X_{e}(e^{j\omega})=\sum\limits_{k=-\infty}^{\infty}x[k]e^{-j\omega Lk}=X(e^{j\omega L})$$

还注意到h[n]除了经过一个内插器外, 还经过了一个时移, 由DTFT的性质我们知道这相当于频域乘以因子$e^{-j\omega}$. 于是我们有:

$$X(e^{j\omega})=G(e^{j2\omega})+e^{-j\omega}H(e^{j2\omega})$$

以上便得到了子序列DTFT与整个序列DTFT的关系, 对于一有限长非周期序列, 我们将引入DFT. 此前我们已经知道:

$$\mathcal{DFT}:X[k]=\sum\limits_{n=0}^{N-1}x[n]W_{N}^{kn}=\sum\limits_{n=0}^{N-1}x[n]e^{-j\frac{2\pi k}{N}n}$$ $$\mathcal{DTFT}:X(e^{j\omega})=\sum\limits_{n=-\infty}^{\infty}x[n]e^{-j\omega n}$$

我们可以把DFT看成是对DTFT一个周期内频率采样得到的, 也就是在$\omega _{k}=\frac{2 \pi k}{N},k=0,1,\cdots,N-1$处的取值. 于是:

$$\begin{align*} X[k]=X(e^{j2\pi k/N})&= G(e^{j(2\pi k/N)2})+e^{-j2\pi k/N}H(e^{j(2\pi k/N)2}) \\ &= G(e^{j\frac{2\pi k}{\frac{N}{2}}})+e^{-j2\pi k/N}H(e^{j\frac{2\pi k}{\frac{N}{2}}}) \\ &= G[k]+W_{N}^{k}H[k] \qquad k=0,1,...,N-1 \end{align*}$$

上式需要注意的是$G[k]$与$H[k]$是长度为$\frac{N}{2}$序列的DFT, 并且两有限长序列暗含着以$\frac{N}{2}$为周期. 如此我们得到了计算最终目标$X[k]$的计算方法, 确切地说是两子序列与因子$W_{N}^{k}$的组合关系, 其展开后即得到之前所述的蝶形计算步骤. 见下图右边部分:

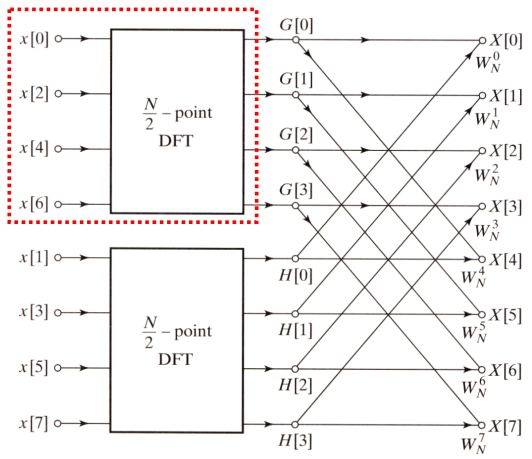
到这里不妨停下来看看经过这样一次拆分, 计算次数是否真的减少了. 基于上次估算的经验, 计算$\frac{N}{2}$个点的$G[k]$需要$(\frac{N}{2})^{2}$次复数乘法和$(\frac{N}{2})(N^{2}-1)$次复数加法, 算上$H[k]$计算量翻倍, 接着和因子$W_{N}^{k}$组合计算又需N次复数乘法与N次复数加法, 累计差不多$N+\frac{N^{2}}{2}$次复数乘法与加法, 而直接计算则是大约$N^{2}$次的复数乘法与加法.

可见计算量有了相当程度的减少, 而这种处理的计算优势才刚刚显现, 当$g[n]$与$h[n]$的样值点数又是2的幂次时, 很自然, 我们能想到再拆分序列以进一步减少计算量. 以$G[k]$为例, 此时$G[k]$在我们眼里即是之前的$X[k]$.

$$\begin{align*} G[k] = \sum\limits_{l=0}^{\frac{N}{2}-1}g[l]W_{\frac{N}{2}}^{lk} &= \overbrace{\sum\limits_{l=0}^{\frac{N}{4}-1} g[2l] W_{\frac{N}{2}}^{2lk}}^{g_{1}[n]DFT} + W_{\frac{N}{2}}^{k}\overbrace{\sum\limits_{l=0}^{\frac{N}{4}-1} g[2l+1] W_{\frac{N}{2}}^{2lk}}^{g_{2}[n]DFT}\\ &= \sum\limits_{l=0}^{\frac{N}{4}-1} g[2l] W_{\frac{N}{4}}^{lk} + W_{\frac{N}{2}}^{k}\sum\limits_{l=0}^{\frac{N}{4}-1} g[2l+1] W_{\frac{N}{4}}^{lk} \\ &= G_{1}[k]+W_{\frac{N}{2}}^{k}G_{2}[k] \\ &= G_{1}[k]+W_{N}^{2k}G_{2}[k] \qquad k=0,1,...,\frac{N}{2}-1 \end{align*}$$

简单说明一下, 这里$g_{1}[n]$与$g_{2}[n]$便是从$g[n]$抽取出来的奇偶序列, 就像从$x[n]$抽取出来$g[n]$与$h[n]$一样. $g_{1}[n]$与$g_{2}[n]$是长度为$\frac{N}{4}$的序列, 且暗含着以$\frac{N}{4}$为周期.

到此我们又能进一步补全蝶形计算流图了.

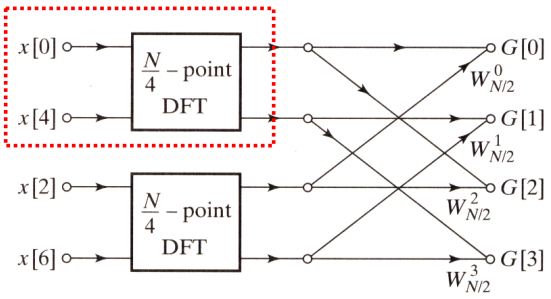
最后看下第一级的运算, 此时是2点DFT, 取x[0], x[4]计算为例:

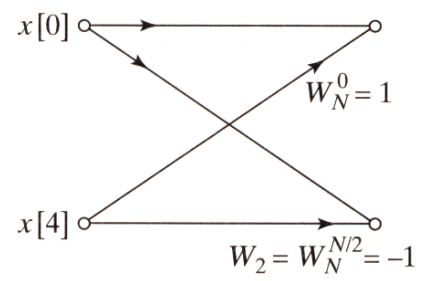
于是整个按时间抽取基2的8点DFT蝶形计算流图就分解完毕了, 如下图:

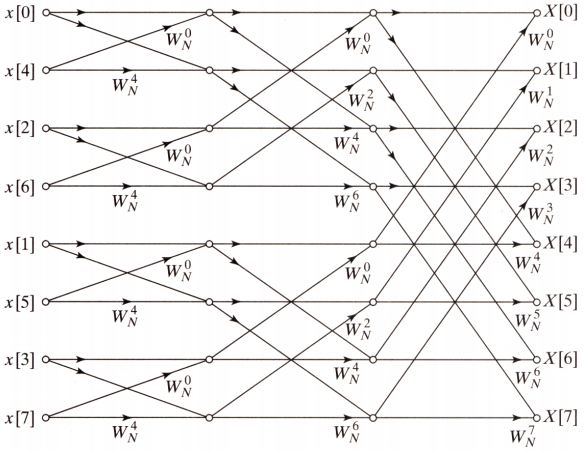
蝶形图不仅清楚地表示出各序列的组合关系, 连计算量也可以很方便估算出来, 因为基本的蝶形计算流图（2点进行DFT）所需的计算量是相同的, 对应两次复数乘法与两次复数加法. 因此只需知道有多少次基本蝶形计算就行了, 而且发现如果序列的长度N为2的幂次, 每一级基本蝶形计算无一例外都需要进行N次, 而最多有$log_{2}N$级, 即需要$Nlog_{2}N$次的复数乘法和复数加法.

还没完, 最后的优化来源于因子$W_{N}^{r}$的对称性和周期性, 具体来说是基于这样的事实: 对于两点经过两个对应旋转因子的组合运算得到两个DFT的值, 而那两个因子的指数部分正相差$\frac{N}{2}$. 正如前面两点蝶形图所示的那样. 于是:

$$W_{N}^{r+\frac{N}{2}}=W_{N}^{\frac{N}{2}}W_{N}^{r}=-W_{N}^{r}$$

因此简化后的基本计算流图变成这个样子:

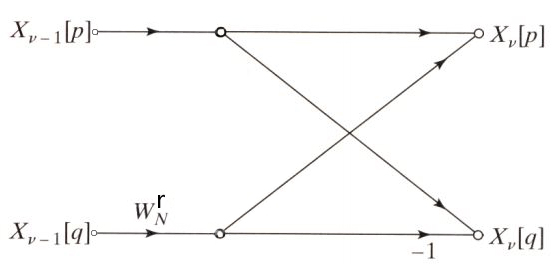
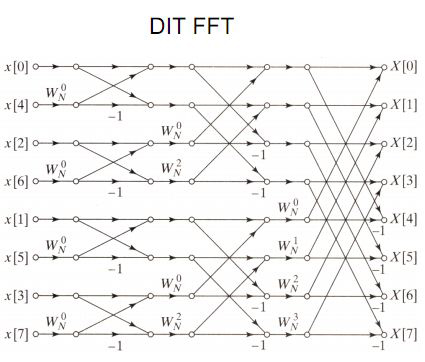
可见化简后基本蝶形图的复数乘法次数变为一次, 从而整体上复数乘法次数减少一半. 完整的8点FFT蝶形图应该如下图:

下面再深入讨论下FFT的计算过程, 以便启发编程实现的思路. 蝶形计算中还潜藏着编程实现FFT的方法, 或者可以说这才是我们真正的目的.

上面蝶形流图表示出的FFT计算过程又被称之为是一种同址计算, 观察一下, 每级基本蝶形图输入$x_{m-1}[p]$、$x_{m-1}[q]$输出$X_{m}[p]$、$X_{m}[q]$, 也就是说新的p、q位置的节点值正是由上一节p、q位置的节点值计算得来的. 这意味着计算N点FFT只需一列存N个点的存储寄存器, 而不必更多, 因为允许我们每计算出一个结果直接覆盖对应位置的输入上(事实上, 由于每个输入计算时都会用到两次, 所以还需要一个寄存器临时存放两个输入中的其中一个). 另一个比较头疼的问题是序列的存取问题, 在如前所述的计算中, 读取计算样值点的位序似乎是“错乱无章”的, 而最终输出的DFT结果序列则是正序的.

这种蝶形计算的读取次序又被称为倒位序, 把输入输出位序以二进制表示可以直观得出这一点. 以8点序列为例, 输入输出序号做如下变化:

$$\begin{array}{|c|c|c|} \hline x[n] & \text{倒位序} & X[k] \\ \hline 0 & x[000] \to X[000] & 0 \\ \hline 4 & x[100] \to X[001] & 1 \\ \hline 2 & x[010] \to X[010] & 2 \\ \hline 6 & x[110] \to X[011] & 3 \\ \hline 1 & x[001] \to X[100] & 4 \\ \hline 5 & x[101] \to X[101] & 5 \\ \hline 3 & x[011] \to X[110] & 6 \\ \hline 7 & x[111] \to X[111] & 7 \\ \hline \end{array}$$

输入序列的位序正好是输入为序的倒序. 其实造成这个原因的本质说也简单, 因为每一级的序列都是按位序的奇偶来分组的, 故可以从二进制表示中看出这一点, 0表示被分到偶序列组, 1表示被分到奇序列组.

到这里我想基2FFT的计算思路及过程细节讲完了, 也对蝶形图有了更深的理解. 通过输入与输出的重新排列组合, 还可以画出很多样式的蝶形图, 比如使输入正序, 输出倒序, 甚至是输入输出都正序（但此时数据即不能顺序存取, 计算也不是同址的, 因此并没有优势）. 受人们关注的还有Singleton在1969年提出的按时间抽取的蝶形计算流图, 其也是通过重排蝶形图内部节点顺序画成的, 最大的特点是每一级的几何形状都相同, 这使数据顺序存取成为可能. 见下图:

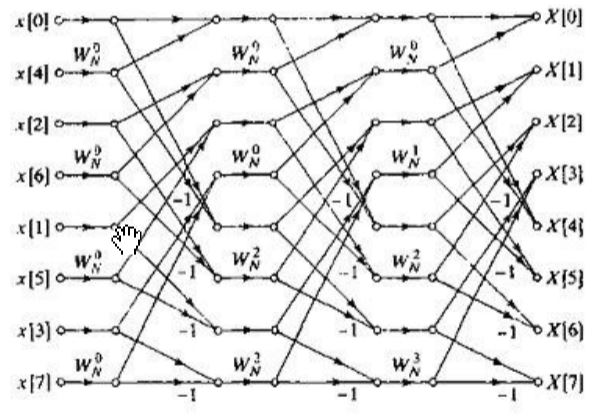
除此之外, 对于不同的序列长度, 还有基-3、基-4以及分裂基的一些FFT算法, 以及另外一些不同角度或思路快速计算DFT的方法, 比如按频率抽取的FFT、Winograd傅里叶变换算法等等. 有机会必定再深入研究下.

本文大多数蝶形图取自维基百科库利－图基快速傅里叶变换算法词条.

参考: 《离散时间信号处理（第三版）》Alan V. Oppenheim, Ronald W. Schafer 著.

.
.
.
.
.
.
.
終わり